The ubiquitous use of math in everyday life demands that you understand the mathematical formulas used in the class of 7. Many students need help in math due to difficulties in mastering the recipes.
This article will guarantee that students don’t have to learn the formulas in class 7 by describing them most simply and providing practical tips that can be incorporated into daily routines that aid students long-term.

Use negative figures.
Please find the relation between proportions and use them to calculate rates or unit costs. Use tables and graphs to determine whether different quantities are proportional.
Use all four operations (+ (-, + ) (x, + (x, x, -,) concerning fractions, decimals, as well as percentages for various types of problems.
Solve algebraic problems and equations using a minimum number of variables (unknown quantity).
Fluidly converts decimals to fractions (and the reverse) and then puts them on a number line.
Use scale drawings and formulas to resolve real-world situations that require the volume, area, and area of two – or three-dimensional models.
Learn the formulas used to calculate a circle’s circumference and area.
Discover the basics of sampling random and use results to draw general conclusions about two groups.
Develop as well as probabilistic test models.
Negative number Negative numbers
The children learn that numbers and their reverses, like 7 and -7, can be described as “additive inverses,” which means that when mixed, they’re the same as the total of the numbers 0.
Students learn that an expression like p + Q is an integer in the line when solving equations. It is possible to have the numbers either in the positive or negative position.
Additionally, children must understand that subtracting numbers is similar to removing their opposite (aka negative number).
For example, the combination of A and b is a”b.
When it comes time for multiplication, students will be able to understand the patterns of numbers appearing in negative patterns when negative numbers are utilized. In other words, multiplying a positive and a negative one results in a negative. The outcome is positive if you multiply two numbers that can be negative in their sum.
For example, 2 x -2 = 4 and 2 x 2 = 4.
For example, 4×4=16 and 4×4=-16.
Examples
Samantha had an outstanding debit balance on her credit card of just $50 in her bank account. Samantha received her monthly payment of $500and she decided to withdraw $200 in cash. What’s the amount of funds Samantha has in her performance at the bank?
To determine the root of to solve the issue, we start with the initial balance of Samantha of $50, which is minus. Because her balance is zero, so she is in debt to the bank for the amount. Let’s add her earnings of $500 to that amount:
-$50 + $500 = $450
After she has received her pay, Samantha’s balance grows to $450. However, she chooses to take out $200 by taking $200 out of her account:
$450 – $200 = $250
After she has taken out the $200, Samantha has $250 left in her performance.
Certainly! Below is an example of a negative number suitable for 7th grade:
Sarah is currently hiking through the mountains. She starts her journey at a height 500m higher than sea level. Then, she starts to descend. Every 100 meters she is at, the elevation falls to around 20m. If Sarah continues to drop at the same level, then what will the peak of her at the lower end be at 400m?
To tackle this issue, we’ll utilize negative numbers to indicate the reduction in elevation. It is assumed that negative numbers represent downward motion.
Sarah starts the journey from an altitude of 500m above sea level. Because she’s in the process of descending to sea level, we’ll assign a negative sign for her elevation.
Initial elevation 500m
For every 100 meters Sarah descends, her elevation drops by 20 meters. To determine the amount of height she’s losing after 400 meters of descent then, multiply 400 times 100, then, following that, multiply by 20.
Lower elevation: (400 / 100) * 20 = 4 * 20 = 80 meters
We are now able to subtract the drop in elevation by subtracting her altitude at the start:
Final elevation (80 meters) equals 580m
So, after climbing 400 meters, Sarah’s elevation stands at -580m above sea level.
Watch this video to find out what information seventh graders should be aware of when using negative math numbers and using the numbers line.
Be sure that it is proportional.
7th graders use proportions which require complicated fractions to solve problems that require ratios and rates.
For example, When Jackson consumes 1.2 pies in one-fifth of an hour, what is the rate at which he eats pie? Six pies in an hour is the correct answer.
Significant new skills to learn this year can be the capacity to identify the proportionality of two numbers using tables, equations, and graphs using the coordinate plane.
An excellent example of an Equation, for instance: If two T-shirts cost $9 and eight T-shirts run $36, the Equation that describes the cost and amount of products in both scenarios can be written as follows: Equation: t=pn and the Equation is total = price x. When you add these figures, the cost of one T-shirt is the same, indicating the ratio is inverse.
2 9 x T = 2. Thus, one shirt is $4.50.
8 x T = 36, so one T-shirt is $4.50.
If the graph can be described as a straight line that is a straight line that runs through the “0,0” point of the plane point, the quantities are proportional.
Algebra Inequalities and Equations
Which algebraic concept is it? This may help:
Algebra solves mathematical issues (such as 35 = -2.5 + 3.5x) or equations (such as 1011 > the number x) by using one or more variables (unknown number).
Also, the term expression can be described as an equation, however, without answers or the sign of equals. It’s a term in numerical form that describes a number, like 3x-2. What’s the formula? 3x -2 = 13.
Seventh-grade students work on equations, expressions, and inequalities using only one variable.
Seventh graders realize the possibility of writing the expression in an alternate style will make it easier to complete a task.
For example, 0.05a+a can be written as 1.05a, which translates to “increase by 5%” or “multiply by 1.05.”
This year, resolving multi! Step issues can be more difficult due to problems involving negative numbers, decimals, fractions, percentages, rates, and more. These issues may require graphing of data to solve. Solutions could be inequalities instead of being able to provide a solution.
In the following illustration: Steve is a shoe salesperson and is paid $500 weekly, in addition to $4.50 for every pair of shoes he sells. Steve would like to earn the amount required to cover rent this week of $1700 and has a reduction of about 60. How many pairs of shoes will Steve create this
Also Read: Types of A Specific Formula for Solving a Problem Is Called

Area Volume, Area, and the circumference
Seventh graders are working on increasingly complex shapes. They draw scale drawings of different forms to determine the volume and area, grasp aspects like angles, and learn how to break bodies into pieces to understand them better. Your child could “unfold” a three-dimensional shape such as a pyramid, then transform it into an oddly-shaped 2-dimensional model expected to explain and quantify its attributes. Through these games, your child, who is in the seventh grade, becomes proficient in using rulers, protractors, and other tools. He may even use technology-based tools, like software that allows drawing at scale.
Geometry also has a stunning appearance. Your child must recall the formulas for determining a circle’s circumference and size (A will be pr two and C = 2pr, for example). Also, she should be able to utilize additional, complementing verticals and other angles to determine the angle unknown for a right-angled prism triangle or another polygon. This is vital in solving real-world problems requiring quadrilaterals, triangles, polygons, and cubes, cubes, and the right and left prisms.
What’s the chance?
Did your seventh-grade maths teacher frequently flip coins and record the results? If so, it’s a component of seventh-grade maths that may be familiar to you. Your child in this grade will be expected to grasp the basic probability concepts, including random sampling. Then, using this information to develop the idea of”representative samples. “representative sample.”
For example, to determine who will win the upcoming school election, students can take small samples of poll information and decide who will be the winner based on the amount of data collected and the results from the survey.
They also have to assess information and draw inferences from two types of groups.
For instance, students could measure the total heights of players on the soccer team and all players on the tennis team and record those measurements to identify the differences and similarities between the two groups.
In seventh-grade math, kids will learn to build using probabilities and then analyze the results. In this way, you can aid your child in anticipating the significance of all sorts of life situations. Which basketball team will they be rooting for to be able to make the playoffs? She’ll be able to figure out the chances on her own. Is his favorite artist going platinum? He can estimate the probability from recent sales figures
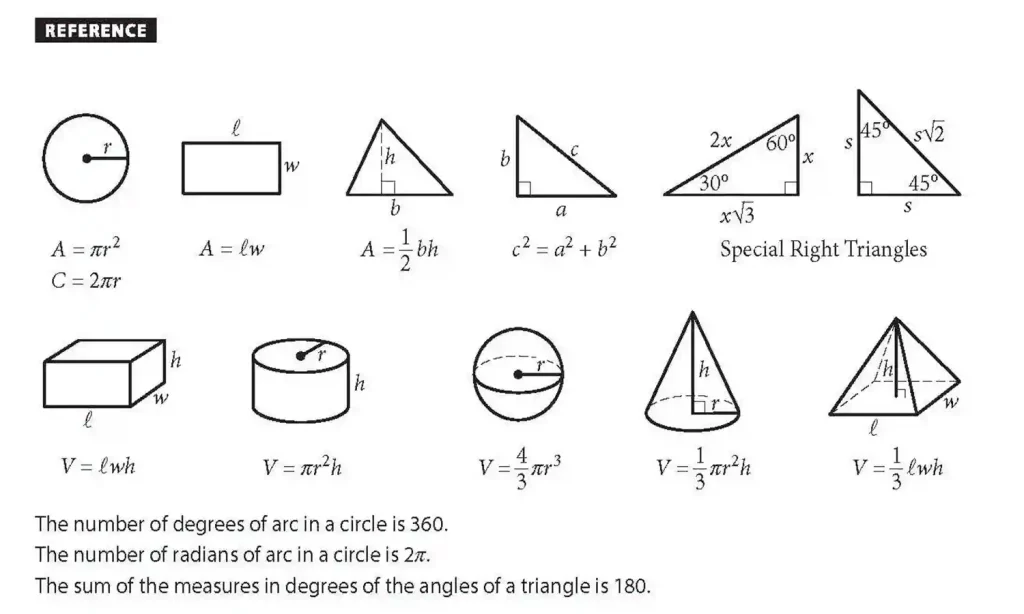
List of Important Maths Formulas for Class 7
An x or one is an x-y
- one /b x = one one one /b equals (a/b) x
- (a x) y = a xy
- (a-b-c)2 = a2 + b2 + c2 – 2ab + 2bc – 2ac
- Increase in Percentage = (Change / Original Amount ) x 100
- Profit percent = (Profit / Cost price) x 100
- Simple Interest = (Principal x Rate x Time) / 100
- Amount = Principal + Interest
- Pythagoras Theorem : (Hypotenuse) 2 = (Adjacent Side) 2 + (Opposite Side) 2
- The area of a circle is 2, with “r” as the circle’s radius, and p is equal to 22/7 or 3.14
Rational Numbers Class 7 Math Formulas
This collection of numbers of rationals used in formulas used in math class 7 assists students in getting an idea of how math calculations use rational numbers.
Rational number Products = (Product of Numbers) (Product of Numerators) (Product of Numerators)
The first Rational number will be x (Reciprocal of a different Rational Number)
Practical Geometry Class 7 Math Formulas
The shapes we see around us are important and significant in our daily lives. Thus, the practical geometry math formulas taught in class 7 assist students in understanding the shapes they create and the mathematical calculations that go along with the dimensions of their bodies.
- Area of a Square = Side 2
- The perimeter of a Square = 4 x Side
- Area of Rectangle = Length x Breadth
- Perimeter of a Rectangle = 2 x (Length + Breadth)
- Area of a Parallelogram = Base x Height
- Area of Triangle = 1/ 2 x Base x Height
- The circle’s circumference can be calculated as p “d,” which is the circle’s circumference. it is 22/7, which is 3.14
- Circle’s surface is 2 per 2
Exponents and Power Formulas for Class 7 Maths
An exponent is a figure that describes the number of times a specific quantity has been multiplied. For example, 4 four x 4 = 4. This could also be written in 3. For instance. This is because four is the basis, and the third can be described as an exponent. Formulas (laws) related to exponents assist in carrying out many operations in the face of massive numbers. Here is a listing of the various exponent laws that are employed:
- Law of Product: a m x a n = a m+n
- Law of Quotient: a m/a n = a m-n
- Law of Zero Exponent: a 0 = 1
- Law of Negative Exponent: a -m = 1/a m
- Law of Power of a Power: (a m) n = a mn
- Law of Power of a Product: (ab) m = a mb m
- Law of Power of a Quotient: (a/b) m = a m/b m
- Comparing Quantities Formulas for Class 7 Maths
Every day, we face situations that require us to evaluate two things. It can be things like wages, weights, and grades, as well as grades. It is, therefore, essential to be aware of the concept of proportions and ratios. The ratio is the term used to compare two numbers in identical units. This is the opposite includes the measure of a particular amount.
If two ratios are required to be compared, this can be achieved by converting them into similar fractions. Two ratios are equivalent when both bits are comparable.
The numbers are deemed to be proportionate for any four digits if their ratios match.
Increase in Percentage = (Change / Original Amount ) x 100
Profit percent = (Profit / Cost price) x 100
Simple Interest = (Principal x Rate x Time) / 100
Amount = Principal + Interest
Algebra Formulas for Class 7 Maths
Variables and constants are employed in algebraic equations. The algebraic units below will help students understand variables and constants that require subtraction or added, then multiplied to form an algebraic equation.
This numerical word is known as the coefficient.
Similar terms are added when adding two algebraic equations, while those that aren’t similar remain precisely the same.
(a-b)2 = a2 – 2ab + b2
(a-b-c)2 = a2 + b2 + c2 – 2ab + 2bc – 2ac
Applications of Class 7 Maths Formulas
The math formulas taught in class 7 comprise the most fundamental and valuable recipes that can be useful across various areas.
Math formulas for class 7 assist in understanding the workings of everyday tasks. It doesn’t matter if the job is the analysis of profit or losses or the calculation of interest on money. The formulas can be used across the globe.
The measurement and geometry formulas help calculate the dimensions of the shapes we see daily. For example, when someone wants to determine the number of bricks required to construct rooms, the knowledge of geometric formulas could be utilized.
Formulas for algebra give us the ability to find unknown values. Every issue that requires an undefined variable could be solved by treating it as an algebraic equation. By using algebraic entities, the problem can be solved quickly.
Class 7 Maths Formulas Examples
Example 1: The Cost price of the bag is Rs. 250. If the product is sold for Rs. 300, compute the profit earned and the profit percentage.
Solution:
Cost Price of the bag = Rs. 250. The selling price is 300 rupees. 300
If the selling price is higher than the price at which the item was bought, it is possible to profit from selling. Profit = Selling Price = Cost Price
Substituting values from the equation Profit = 300 x 250 = 50
Profit percentage = (Profit /Cost price) x 100
Substituting values using that formula, the percentage of profit equals (50/250) 100 multiplied by 100 is 20/20 percent. Thus the rate of profit is 20%.
Example 2. What is the size of a rectangle with ten units of width and length (width) of five teams?
Solution :
The size of a rectangle is the length of the rectangle and width Breadth
A wall’s size is 10×5, which is equivalent to fifty units.
Also Read: Derivation of A Square Minus B Square With Example
The rectangle’s surface comprises 50 units of space.
List of Important Maths Formulas for Cl
- Area of a Square = Side 2
- Perimeter of a Square = 4 x Side
- Area of Rectangle = Length x Breadth
- Perimeter of a Rectangle = 2 x (Length + Breadth)
- Area of a Parallelogram = Base x Height
- Area of Triangle = 1/ 2 x Base x Height
- The circumference of the arcuate can be calculated as p, where “d” is the circumference of an arc. It is 22/7, which is 3.14
- Circle’s surface is 2. 2
Exponents and Power Formulas for Class 7 Math’s
An exponent is the term used to describe a number that is the amount of times that a particular amount has been multiplying. For instance, 4 x 4 x 4. This could also be written in 3. For instance.. This is due to the fact that four is the basis and the third can be described as an exponent. Formulas (laws) related to exponents help in the execution of many operations in the face of massive numbers. Here is a listing of the various exponent laws which are used:
- Law of Product: a m x a n = a m+n
- Law of Quotient: a m/a n = a m-n
- Law of Zero Exponent: a 0 = 1
- Law of Negative Exponent: a -m = 1/a m
- Law of Power of a Power: (a m) n = a mn
- Law of Power of a Product: (ab) m = a mb m
- Law of Power of a Quotient: (a/b) m = a m/b m
Comparing Quantities Formulas for Class 7 Maths
Everyday, we face situations which require us to evaluate two things. It could be weights and wages, grades, and even the grades. It is therefore essential to know the difference between proportions and ratios. Ratio refers to the comparing between two numbers in identical units. It signifies the amount of one amount is included in the other.
If two ratios need to be compared the process can be made by converting them into similar fractions. Two ratios are equivalent if both fractions are comparable.
For any four numbers if their ratios are equal, the numbers are deemed to proportional.
- Increase in Percentage = (Change / Original Amount ) x 100
- Profit percent = (Profit / Cost price) x 100
- Simple Interest = (Principal x Rate x Time) / 100
- Amount = Principal + Interest
Algebra Formulas for Class 7 Maths
Variables and constants are used in algebraic equations. The algebraic units below can assist students in learning about variables and constants that need to be subtracted from, multiplied and added in order to formulate this algebraic equation.
The value numerical of this term is called the coefficient.
In the case of adding two algebraic equations, the terms that are similar are added. Those that are not related are treated exactly the same way.
- (a-b)2 = a2 – 2ab + b2
- (a-b-c)2 = a2 + b2 + c2 – 2ab + 2bc – 2ac
Applications of Class 7 Maths Formulas
7th grade math formulas Math formulas used in the Class 7 are the most fundamental and practical formulas useful across many subjects.
Math formulas for class 7 help students understand the inner workings of daily activities. It doesn’t matter if the task is the analysis of profit or losses, or the calculation of interest rates for money. The formulas can be used across the globe.
Mensuration and geometry formulas assist in calculating dimensions of shapes we see everyday. For example If someone needs to know the amount of bricks required for building an area, then understanding of geometric formulas could be utilized.
Algebraic formulas give us the ability to discover unknown value. Anything that has an undefined variable could be resolved by placing it in the form of an equation algebraic. By using algebraic entities, the problem can be easily solved.
Class 7 Maths Formulas Examples
Example 1: The Cost price of the bag is Rs. 250. If it’s sold for Rs. 300, compute the profit and also the percentage of profit.
Solution:
- Cost Price of the bag = Rs. 250. Selling price is 300 rupees. 300
- Since selling prices are higher than the price at which the item was bought There is a profit made from selling. Profit = Selling Price = Cost Price
- Substituting values from the Formula Profit =300 x 250 = 50
- Profit percentage = (Profit /Cost price) x 100
- Substituting values using that formula, the percentage of profit equals (50/250) 100 times 100 equals 20/20 20%. Therefore the percentage of profit is 20% .
Example 2.What is the size of a rectangle that has width 10 units as well as length (width) five units?
Solution :
The area of a rectangle can be described as the length of the rectangle length x Breadth
The area of one wall is 10×5 which is equal to 50 units. The rectangular surface comprises 50 units.






