Types of A Specific Formula For Solving A Problem Is Called

 Understanding the Basics

1

Understand the difference between an algebraic expression and an algebraic equation. An algebraic expression is a mathematical phrase containing numbers and variables. It does not have an equals sign and cannot be solved. However, An algebraic equation can be solved and includes a series of algebraic expressions separated by an equals sign. Here are some examples: 

• Algebraic expression: 4x + 2
• Algebraic equation: 4x + 2 = 100

2

Know how to combine like terms. Combining like terms means adding up (or subtracting) the terms of the same degree. This means that all x2 terms can be combined with other x2 terms, that all x3 terms can be combined with x3 terms, and that all constants, numbers that are not attached to variables, such as 8 or 5, can be added up or combined. Here’s an example:[2]

• 3×2 + 5 + 4×3 – x2 + 2×3 + 9 =
• 3×2 – x2 + 4×3 + 2×3 + 5 + 9 =
• 2×2 + 6×3 + 14

3

Know how to factor a number. If you’re working with an algebraic equation, which means there is an expression on either side of an equal sign, then you can simplify it by factoring out a common term. Look at the coefficients of all of the words (the numbers before the variables or the constants) and see if there is a number that you can “factor out” by dividing each time by that number. If you can do this, you have simplified the equation and are on your way to solving it. Here’s how: 

• 3x + 15 = 9x + 30
• You can see that each coefficient can be divisible by 3. To get your simplified equation, just “factor out” the number 3 by dividing each term by 3.
• 3x/3 + 15/3 = 9x/3 + 30/3 =
• x + 5 = 3x + 10

4

Know the order of operations. The order of operations, also known by the acronym PEMDAS, explains the order in which you should perform different mathematical functions. The order is Parentheses, Exponents, Multiplication, Division, Addition, and Subtraction. Here’s an example of how the order of operations works: 

• (3 + 5)2 x 10 + 4
• First, follow P, the operation in the parentheses:
• = (8)2 x 10 + 4
• Then, follow E, the operation of the exponent:
• = 64 x 10 + 4
• Next, do multiplication:
• = 640 + 4
• And last, do addition:
• = 644

5

1. Learn how to isolate a variable. If you’re solving an algebraic equation, your goal is to get the variable, often known as x, on one side of the equation while placing the constant terms on the other side. You can isolate x by division, multiplication, addition, subtraction, finding the square root, or other operations. Once you’ve isolated x, you can solve it. Here’s how: 
2. 5x + 15 = 65 =
3. 5x/5 + 15/5 = 65/5 =
4. x + 3 = 13 =
5. x = 10

1. Solution(By Examveda Team)
2. A step-by-step procedure used to solve a problem is called Algorithm. An algorithm (pronounced AL-go-rith-um) is a procedure or formula for solving a problem based on conducting a sequence of specified actions.
3.  

Types of Problems

1. In school and everyday life, we all have to solve a wide variety of problems. In school, these problems might be how to complete an algebraic equation or remember the order of U.S. Presidents. In everyday life, problems might be how to maintain a long-distance relationship or how to pay bills on a limited income. Either way, to be successful, we must be able to solve different types of problems using different types of solution strategies.
2. Problem-solving is the application of ideas, skills, or factual information to solve a problem or reach a desired outcome. Let’s talk about different types of issues and other kinds of solutions.
3. Educational psychology has broken down problems in two different ways. The first way is to make a distinction between well-defined and poorly-defined problems. A well-defined problem has a clear goal or solution, and problem-solving strategies are quickly developed. In contrast, a poorly-defined problem is the opposite. It must be clarified, abstract, or described and requires a straightforward problem-solving approach.
4.  
5. Problem-Solving Strategies
6. Depending on the type of problem, you have many options regarding possible solution strategies. In this lesson, let’s start with solutions that are common strategies for well-defined or routine issues.
7. The first strategy you might try when solving a routine problem is called an algorithm. Algorithms are step-by-step strategies or processes for how to solve a problem or achieve a goal. The most common example of using algorithms is in math class. When presented with an algebraic equation, you learn how to solve for x using specific, well-defined steps. But algorithms can be used in other subjects as well. For example, when learning how to take apart and clean a car engine, you will want to approach this problem using a set series of steps to keep all the parts intact.
8. Another solution that many people use to solve problems is called heuristics. Heuristics are general strategies used to make quick, shortcut solutions to issues that sometimes lead to answers but sometimes lead to errors. Heuristics are sometimes called mental shortcuts, and we often form them based on past experiences. You have probably used heuristics, always used heuristics life, without knowing what they are called. For example, when you go to the store to buy a product, several options will probably ben the shelf. When deciding the quality of the different choices, many people use the heuristic rule, ‘you get what you pay for,’ meaning more expensive items will be of higher quality. While this might be true in many cases, it’s not always true. Using strategy makes for a quick decision but could backfire.
9.  

EXAMPLE: SOLVING A VOLUME PROBLEM

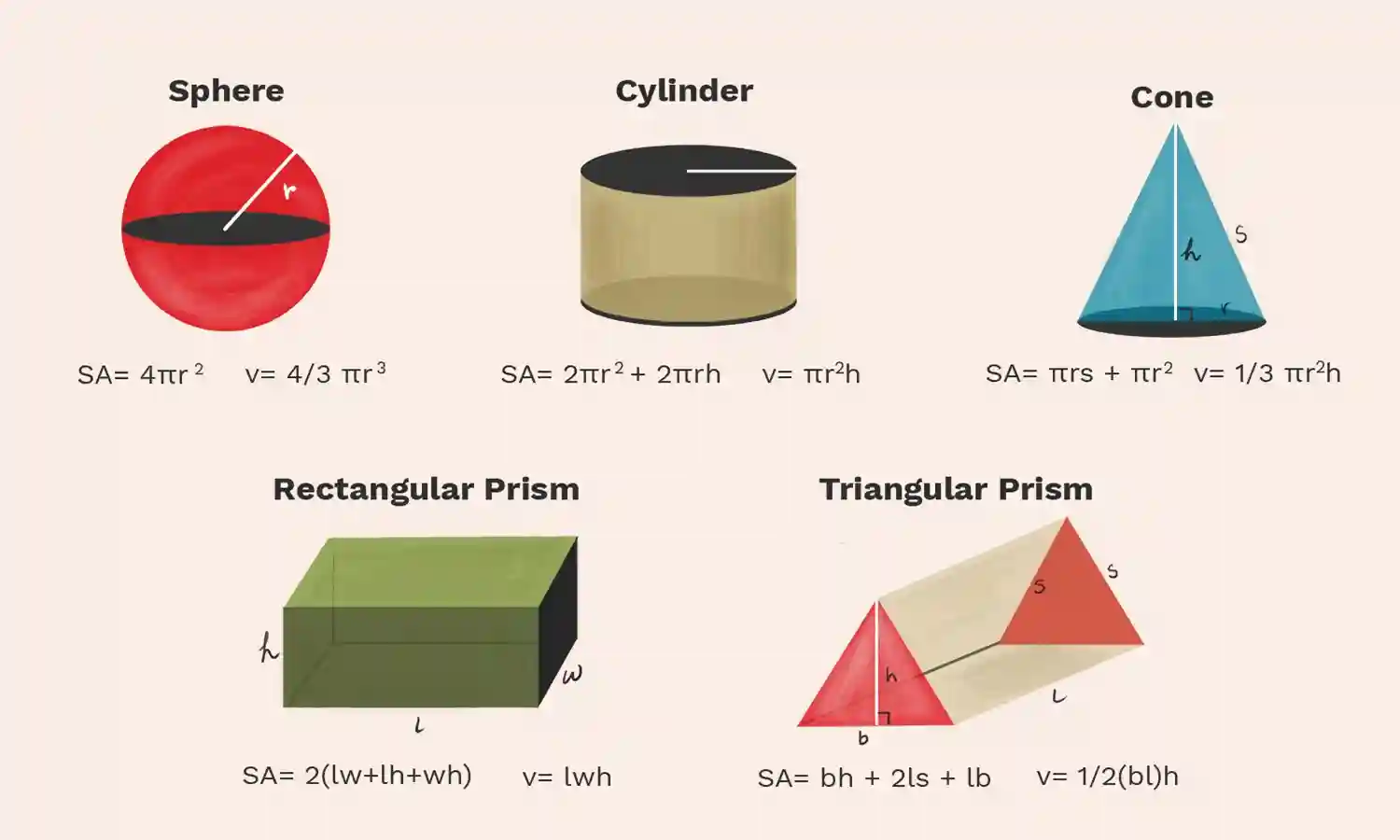
1. Find the dimensions of a shipping box given that the length is twice the width, the height is 88 inches, and the volume is 1,600 in.3.
2. Show Show Solution
3. The formula for the volume of a box is given as V=LWH, the product of length, width, and height. We are blessed that L=2W and H=8. The book is 1,600 cubic inches.
4.  
5. V=LWH
6. 1,600=(2W)W(8)
7. 1,600=16W2
8. 100=W2
9. 10=W
10. The dimensions are L=20in., W=10 in., and H=8 in.

Analysis of the Solution

1. Note that the square root of W2 would result in a positive and a negative value. However, we can use only the positive result because we are describing width.
2.  
3.  
4. EXAMPLE: SOLVING AN AREA PROBLEM
5. The perimeter of a tablet of graph paper is 48 in. The length is 66 in. more than the width. Find the area of the graph paper.
6. Show Show Solution
7.  
8.  
9. The standard formula for area is A=LW; however, we will solve the problem using the perimeter formula. We use the perimeter formula because we know enough information about the perimeter that the procedure will allow us to solve for one of the unknowns. As both perimeter and area use length and width as dimensions, they are often used together to solve a problem like this.
10. We know the length is six in. more than the width, so we can write the size as L=W+6. Substitute the perimeter’s value and the length expression into the perimeter formula and find the length.
11. P=2L+2W
12. 48=2(W+6)+2W
13. 48=2W+12+2W
14. 48=4W+12
15. 36=4W
16. 9=W
17. (9+6)=L
18. 15=L
19. Now, we find the area given L=15 in. and W=9 in.
20. A=LW
21. A=15(9)
22. =135 in2

1. The area is 135135 in2.
2. When solving word problems with algebraic sentences, the primary key is to translate the algebraic expressions accurately and then set up and write each algebraic equation correctly. In doing so, we can ensure that we are solving the right equation and, as a result, will get the correct answer for each word problem.

Also Read: Best 7th Grade Math Formulas For Children

Solve an Algebraic Equation

A.3 Algebraic Expressions and Problem-Solving

1.  
2. You are familiar with using letters or variables to stand for unknown numbers in equations or formulas. Variables also represent numerical quantities that change over time or in different situations. For example, atmospheric pressure might be at different heights above the Earth’s surface. Or it might represent the number of people infected with cholera days after the start of an epidemic.
3. An algebraic expression is any meaningful combination of numbers, variables, and symbols of operation. Algebraic expressions are used to express relationships between variable quantities.

Example A.17.

• Loren makes $66 an hour working at the campus bookstore.
• Choose a variable for the number of hours Loren works per week.
• Write an algebraic expression for the amount of Loren’s weekly earnings.
• Solution
• Let hℎ stand for the number of hours Loren works per week.
• The amount Loren earns is given by
• 6×(number of hours Loren worked)6×(number of hours Loren worked)
• Or six⋅h. six⋅ℎ. Loren’s weekly earnings can be expressed as six h.

A.3 Algebraic Expressions and Problem-Solving

1.  
2. You are familiar with using letters or variables to stand for unknown numbers in equations or formulas. Variables also represent numerical quantities that change over time or in different situations. For example, atmospheric pressure might be at different heights above the Earth’s surface. Or it might represent the number of people infected with cholera days after the start of an epidemic.
3. An algebraic expression is any meaningful combination of numbers, variables, and symbols of operation. Algebraic expressions are used to express relationships between variable quantities.

Example A.17.

1. Exercises A.3
2. For Problems 1-12, write algebraic expressions to describe the situation and then evaluate the given values.

1

1. Jim was 27 years old when Ana was born.
2. Write an expression for Jim’s age in terms of Ana’s age.
3. Use your face to find Jim’s age when Ana is 22.

1.  
2. Rani wants to replace the wheels of her in-line skates. New wheels cost $6.59 each.
3. Write an expression for the total cost of new wheels regarding the number of spins Rani must replace.
4. Use your expression to find the total cost if Rani must replace eight wheels.
5. 3.
6. Helen decides to drive to visit her father. The trip is a distance of 1260 miles.
7. Write an expression for the total number of hours Helen must drive in terms of her average driving speed.
8. Use your expression to find how long Helen must drive if she averages 45 miles per hour.
9. 4.

1.  
2. Ben will inherit one million dollars on his twenty-first birthday.

• Write an expression for the number of years before Ben gets his inheritance in terms of his present age.
• Use your face to find how long Ben must wait after he turns 13.

5.

1.  
2. The area of a circle is equal to π times the square of its radius.

• Write an expression for the size of a circle in terms of its radius.
• Find the size of a circle whose radius is 5 centimeters.

6.

1. The volume of a sphere is equal to 43π times the cube of the radius.

• Write an expression for the importance of a sphere in terms of its radius.
• Find the importance of a sphere whose radius is 5 centimeters.

7.

1. The sales tax in the city of Preston is 7.9%.

• Write an expression for the total bill for an item (price plus tax) in terms of the item’s price.
• Find the total bill for a commodity whose price is $490.

8. 

1. A savings account pays 6.4% annual interest on the amount deposited.

• Write an expression for the balance (initial deposit plus interest) in the report after one year in terms of the amount deposited.
• Find the total amount in the account after one year if $350 was deposited.

9.

1.  
2. Your best friend moves to another state. To call her, a long-distance phone call costs $1.97 plus $0.39 for each minute.

• Write an expression for the cost of a long-distance phone call regarding the number of minutes.
• Find the cost of a 27-minute phone call.

10.

1.  
2. Arenac Airlines charges 47 cents per pound on its flight from Omer to Pinconning for passengers and luggage. Mr. Owsley wants to take the flight with 15 pounds of luggage.

• Write an expression for the flight cost regarding Mr. Owlsley’s weight.
• Find the cost of Mr. Owsley’s weight of 162 pounds.

11.

1.  
2. Juan buys a 50-pound bag of rice and consumes about 0.4 pounds per week.

• Write an expression for the amount of rice Juan has consumed in terms of the number of weeks since he bought the bag.
• Write an expression for the amount of rice Juan has left regarding the number of weeks since he bought the bag.
• Find the amount of rice Juan has left after six weeks.

12.

1.  
2. Trinh is bicycling down a mountain road that loses 500 feet in elevation for each 1-mile roadway. She started at a height of 6300 feet.

• Write an expression for the elevation that Trinh has lost regarding the distance she has cycled.
• Write an expression for Trinh’s elevation regarding how many miles she has cycled.
• Find Trinh’s elevation after she has cycled 9 miles.

1. For Problems 13-28, write and solve an equation to answer the question.

13.

1.  
2. Celine’s Boutique carries a jewelry line made by a local artists’ co-op. If Celine charges p dollars for a pair of earrings, she can sell 200−5p200−5 pairs per month. On the other hand, the co-op will provide her with 56+3p56+3 pairs of earrings when she charges p dollars per pair. What price should Celine set so the demand for earrings equals her supply?

14.

1.  
2. Curio Electronics sells garage door openers. If it charges p dollars per unit, it sells 120−p120 openers monthly. The manufacturer will supply 20+2p20+2 openers for p dollars each. What price should Curio Electronics charge so that its monthly supply will meet its demand?
3. 15.
4.  
5. Roger sets out on a bicycle trip at an average speed of 16 miles per hour. His wife finds his patch kit on the dining room table six hours later. If she heads after him in the car at 45 miles per hour, how long will it be before she catches him?
6. What are we asked to find in this problem? Assign a variable to represent it.
7. Write an expression for your variable for the distance Roger’s wife drives.
8. Write an expression for your variable for the distance Roger has cycled.
9. Write an equation and solve it.
10. 16.
11.  
12. Kate and Julie set out in their sailboat on a straight course at 9 miles per hour. Two hours later, their mother becomes worried and sends their father after them in the speedboat. If their father travels 24 miles per hour, how long will it be before he catches them?
13. What are we asked to find in this problem? Assign a variable to represent it.
14. Write an expression for your variable for the distance Kate and Julie sailed.
15. Write an expression for your variable for the distance their father traveled.
16. Write an equation and solve it.
17. 17.
18.  
19. The reprographics department has a choice of 2 new copying machines. One sells for $20,000 and costs $0.02 per copy to operate. The other markets cost $17,500, but their operating costs are $0.025 per copy. The repro department decides to buy the more expensive machine. How many copies must the repro department make before the higher price is justified?
20. What are we asked to find in this problem? Assign a variable to represent it.
21. Write an expression in terms of your variable for the total cost incurred by each machine.
22. Write an equation and solve it.
23. 18.
24.  
25. Annie needs a new refrigerator and can choose between two models of the same size. One model sells for $525 and costs $0.08 per hour. A more energy-efficient model sells for $700 but runs $0.05 per hour. If Annie buys the more expensive model, how long will it be before she starts saving money?
26. What are we asked to find in this problem? Assign a variable to represent it.
27. Write an expression in terms of your variable for the total cost incurred by each refrigerator.
28. Write an equation and solve it.
29. 19.
30.  
31. The population of Midland has been growing at an annual rate of 8% over the past five years. Its present population is 135,000.
32. Assuming the same growth rate, what do you predict for the population of Midland next year?
33. What was the population of Midland last year?
34. 20.
35.  
36. The annual inflation rate has been 6% for the past three years. This year, a steak dinner at Benny’s costs $12.
37. Assuming the same inflation rate, what do you predict for the price of a steak dinner next year?
38. What did a steak dinner cost last year?
39. 21.
40.  
41. Virginia took a 7% pay cut when she changed jobs last year. What percent pay increase must she receive this year to match her old salary of $24,000?
42.  
43. Clarence W. Networth took a 16% loss in the stock market last year. What percent gain must he realize this year to restore his original holdings of $85,000?
44. 23.
45.  
46. Delbert’s test average in algebra is 77. If the final exam counts for 30% of the grade and the test average counts for 70%, what must Delbert score on the final exam to have a term average of 80?
47. 24.
48.  
49. Harold’s batting average for the first eight weeks of the baseball season is 0.385. What batting average must he maintain over the last 18 weeks so that his season average will be 0.350 (assuming he continues the same number of at-bats per week)?
50. 25.
51.  
52. A horticulturist needs a fertilizer that is 8% potash, but she can find only fertilizers that contain 6% and 15% potash. How much of each should she mix to obtain 10 pounds of 8% potash fertilizer?
53.   Pounds of fertilizer
54. % potash
55. Pounds of potash
56.  What are we asked to find in this problem? Assign a variable to represent it.
57. Write algebraic expressions in terms of your variable for the amounts of each fertilizer the horticulturist uses. Use the table.
58. Write words for the amount of potash in each batch of fertilizer.
59. Write two different expressions for the amount of potash in the mixture. Now write an equation and solve it.
60. 26.
61.  
62. A sculptor wants to cast a bronze statue from an alloy that is 60% copper. He has 30 pounds of a 45% alloy. How much 80% copper alloy should he mix with it to obtain the 60% copper alloy?
63.   Pounds of alloy
64. % copper
65. Pounds of copper
66.  What are we asked to find in this problem? Assign a variable to represent it.
67. Write algebraic expressions in terms of your variable for the amounts of each alloy the sculptor uses. Use the table.
68. Write expressions for the amount of copper in each batch of alloy.
69. Write two different expressions for the amount of copper in the mixture. Now write an equation and solve it.
70. 27.
71. Lacy’s Department Stores wants to keep the average salary of its employees under $19,000 per year. If the downtown store pays its four managers $28,000 per year and its 12 department heads $22,000 per year, how much can it pay its 30 clerks?
72. a. What are we asked to find in this problem? Assign a variable to represent it.
73. b. Write algebraic expressions for the total amounts Lacy’s pays its managers, department heads, and clerks.
74. c. Write two expressions for the total amount Lacy pays yearly salaries.
75. d. Write an equation and solve it.
76. 28.
77.  
78. Federal regulations require that 60% of all vehicles manufactured next year comply with new emission standards. Major Motors can bring 85% of its small trucks in line with the standards but only 40% of its automobiles. If Major Motors plans to manufacture 20,000 cars next year, how many trucks will it produce to comply with federal regulations?
79. What are we asked to find in this problem? Assign a variable to represent it.
80. Write algebraic expressions for the number of trucks and cars that will meet emission standards.
81. Write two different expressions for the total number of vehicles meeting the standards.
82. Write an equation and solve it.
83. Know how to factor a number. If you’re working with an algebraic equation, which means there is an expression on either side of an equal sign, then you can simplify it by factoring out a common term. Look at the coefficients of all of the terms (the numbers before the variables or the constants) and see if there is a number that you can “factor out” by dividing each term by that number. If you can do this, you have simplified the equation and are on your way to solving it. Here’s how:[3]
84. 3x + 15 = 9x + 30
85. You can see that each coefficient can be divisible by 3. “factor out” the number 3 by dividing each term by 3 to get your simplified equation.
86. 3x/3 + 15/3 = 9x/3 + 30/3 =
87. x + 5 = 3x + 10
88.  
89. Know how to factor a number. If you’re working with an algebraic equation, which means there is an expression on either side of an equal sign, then you can simplify it by factoring out a common term. Look at the coefficients of all of the terms (the numbers before the variables or the constants) and see if there is a number that you can “factor out” by dividing each term by that number. If you can do this, you have simplified the equation and are on your way to solving it. Here’s how:[3]
90. 3x + 15 = 9x + 30
91. You can see that each coefficient can be divisible by 3. “factor out” the number 3 by dividing each term by 3 to get your simplified equation.
92. 3x/3 + 15/3 = 9x/3 + 30/3 =
93. x + 5 = 3x + 10

Conclusion A Specific Formula For Solving A Problem Is Called

“In conclusion, we have embarked on a captivating journey through the fascinating world of ‘The Formula,’ a specific recipe for unraveling the most intricate enigmas and solving complex problems.

Throughout our exploration, we have come to appreciate the profound impact these formulas wield in diverse domains, transcending boundaries and transcending time.

From the elegant simplicity of mathematical equations to the intricacies of scientific laws and the multifaceted algorithms that govern our digital age, ‘The Formula’ has been the driving force behind humanity’s most significant achievements.

It has enabled us to peer into the cosmos, comprehend the laws of nature, and harness the power of technology to reshape our world.

Yet, we have also witnessed that ‘The Formula’ extends far beyond the confines of science and mathematics. It permeates every facet of human existence, guiding our decisions, shaping our understanding of the human psyche, and illuminating the path towards progress and innovation. It is the essence of distilled knowledge, refined through the toil of great minds and celebrated for its universal application.

Moreover, ‘The Formula’ is a testament to the inherent ingenuity and curiosity of humanity. It symbolizes our ceaseless quest for understanding, our relentless pursuit of knowledge, and our indomitable spirit to conquer the unknown.

As we stand on the shoulders of giants who bequeathed these formulas to us, we are also charged with the responsibility to carry the torch of discovery forward, unearthing new formulas that will drive the future generations towards ever-greater heights.

As we bid farewell to this enlightening journey, let us not forget that ‘The Formula’ is not a mere collection of symbols and equations; it embodies the essence of human potential and the pursuit of truth.

So, let us continue to cherish, nurture, and celebrate the power of ‘The Formula,’ for it is through these elegant expressions that we shall continue to unlock the boundless possibilities that lie ahead.

In the grand tapestry of human history, ‘The Formula’ is a luminous thread that connects the past, present, and future. May it forever guide us towards a world brimming with knowledge, wisdom, and understanding.

Let us, as stewards of this incredible legacy, embrace ‘The Formula’ with open arms and embark on a new chapter of human ingenuity and progress.”