Easy Way to Learn A Cubed minus B Cubed

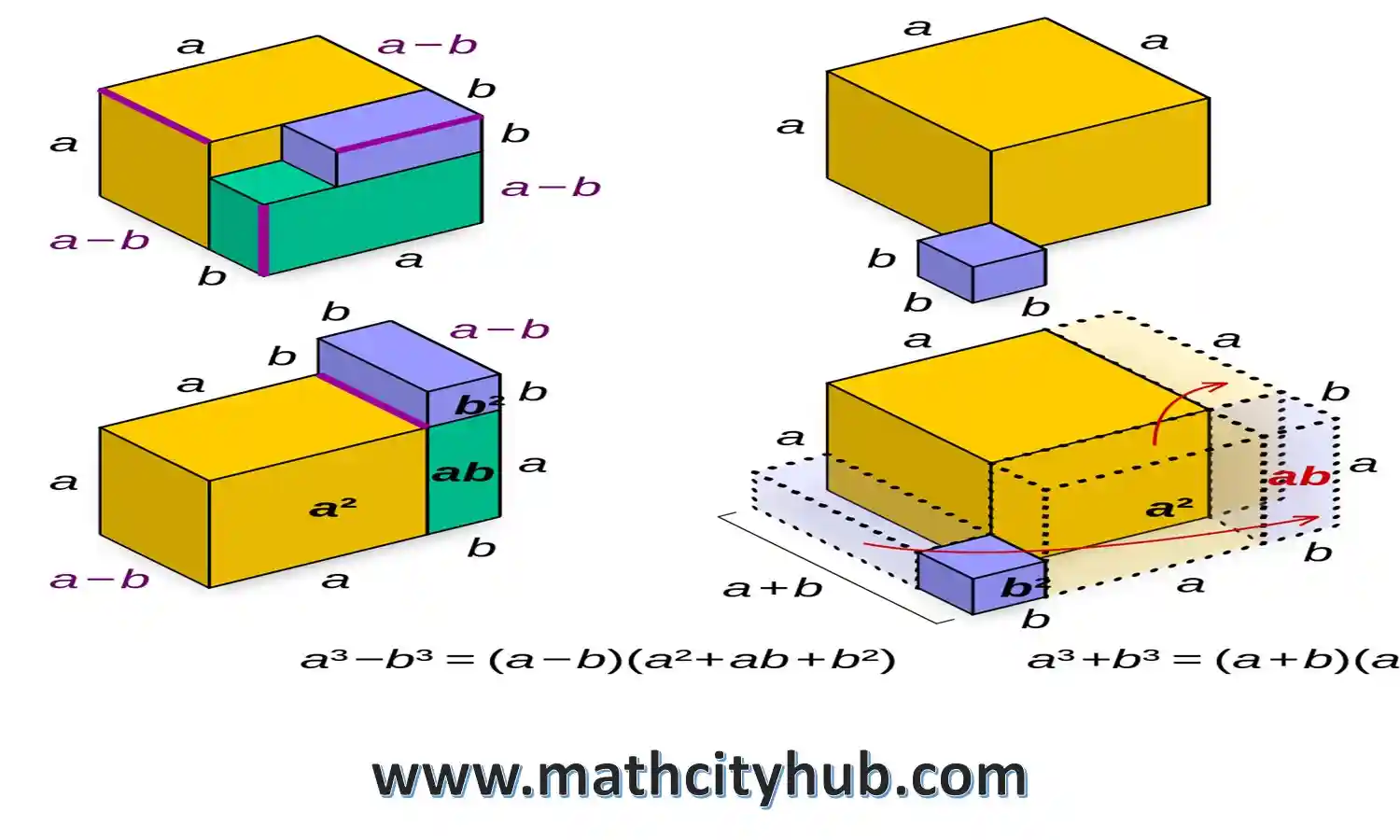
A Cubed minus B Cubed –

In the world of algebraic expressions formulas play an essential function in simplifying complicated mathematical calculations as well as revealing patterns in equations.

One such formula with importance is one that is significant is the “Cube Minus B Cube” formula. This formula is an extremely effective tool for simplifying and expanding expressions that deal with cubes as well as their distinctions.

The Cube Minus B Cube formula offers a simple and elegant illustration of the differences in two cubes. It allows us to understand the complex nature of algebraic formulas by breaking them into simpler components.

With the formula above, mathematical experts as well as enthusiasts alike can quickly analyse and manipulate cube-based equations to unlock their secrets.

The formula itself originates out of the idea that cubing which is the process of raising a number that is expressed to the power of 3. If two cubes, which are represented by a and b are subtracted, their expression can be changed using formula Cube Minus B Cube formula.

With its help by using it, we can simplify the equation and gain valuable insights into the relationships between two cubes.

In this article we will look at how to use the Cube Minus B Cube formula in depth, understanding its structure, and understanding its importance in the field of algebraic manipulation.

We will explore the mathematical basis of its formula, look at the practical applications, and demonstrate its use in a variety of mathematical situations.

At the end of this course you’ll be well-aware of the formula’s capabilities and will be equipped with an effective instrument to simplify and resolve cube-related mathematical equations.

Suggested Read: Types of A Specific Formula For Solving A Problem Is Called

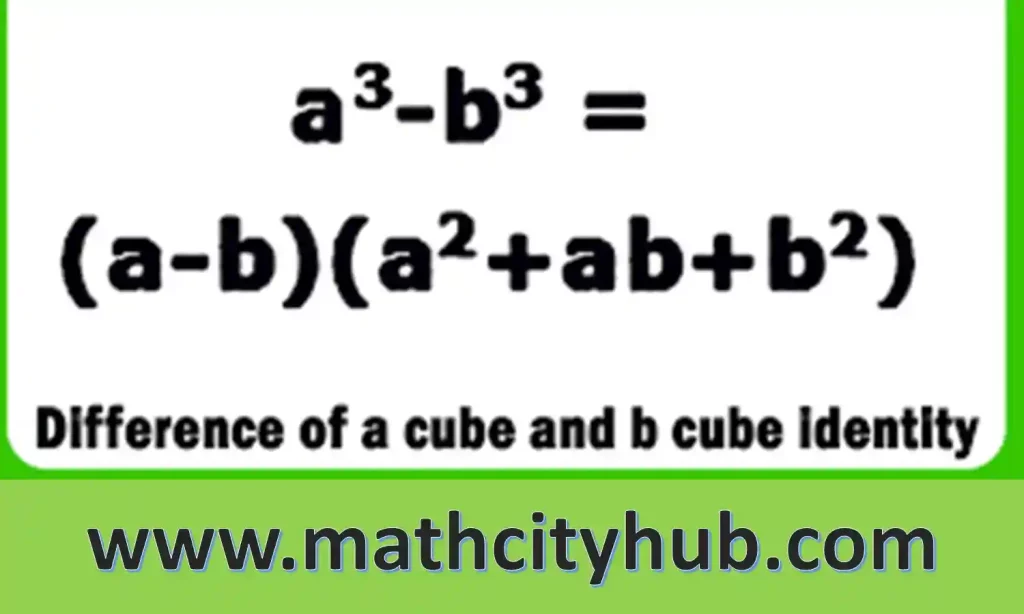
A Cubed minus B Cubed – A cube b cube formula: Explore more about the A cube b cube formula with solved examples

Let’s go on this math-based adventure and find out all the mystery of The Cube Minus B Cube formula.

A cube b cube formula Learn more about the cube b cube formula using solutions to the formula.

TABLE OF CONTENT

• A Cube B Cube Formula
• A Cube Plus B Cube Formula
• B Cube plus B Cube Formula

A Cube B Cube Formula

Cube B Cube Formula can be described as the cube plus b cube formula or a cube plus B cube formula. These formulas can be utilized to solve numerical equations in math.

It can be useful to identify the terms of factorial analysis. It is also a good tool to determine if the two numbers have significant values.

A Cube Plus B Cube Formula

The formula for the cube and b cube has been defined as follows:

a³ + b³ = (a + b)(a² – ab + b²)

This formula can be employed to calculate the total of the cube of two numbers.

a cube plus b cube formula derivation:

As we all know,

(a + b)3 = a3 + 3ab(a + b) + b3

Rewritten as,

a3 + b3 = (a + b)3 – 3ab(a + b)

a3 + b3 = (a + b)[(a + b)2 – 3ab]

a3 + b3 = (a + b)(a2 + 2ab + b2 – 3ab)

a3 + b3 = (a + b)(a2 – ab + b2).

A Cube plus B Cube Formula

The formula for the cube plus the b cube can be defined by,

a³ – b³ = (a – b)(a² + ab + b²)

This formula can be used to calculate the difference of the cube of two numbers.

A Cube and the B Cube Formula

As we all know,

(a – b)3 = a3 + 3ab(a – b) – b3

Rewritten as,

a3 – b3 = (a – b)3 + 3ab(a – b)

a3 – b3 = (a – b)[(a – b)2 + 3ab]

a3 – b3 = (a – b)(a2 – 2ab + b2 + 3ab)

a3 – b3 = (a – b)(a2 + ab + b2).

Solved Examples

Example 1:

Simplify: 54³ + 10³

Solution:

54³ + 10³,

Here a = 54 and b = 10,

Utilizing the formula,

a³ + b³ = (a + b)(a² – ab + b²),

54³ + 10³ = (54 + 10)[(54)² – (54)(10) + (10)³]

= 64(2916 – 540 + 1000)

= 64(3376)

= 216064

Example 2:

Simplify: 9³ – 5³

Solution:

9³ – 5³,

Here a = 9 and b = 5,

Utilizing the formula,

a³ – b³ = (a – b)(a² + ab + b²),

9³ – 5³ = (9 – 5)[(9)² + (9)(5) + (5)²]

= 4(81 – 45 + 25)

= 4(61) = 244

a^3 – b^3 Formula

The formula of a ³ – ³ formula is known as the cube difference (of two figures) formula. The a cube plus b cube formula can be used to calculate the difference between two cubes without actually measuring the cubes.

Additionally, it can be utilized to factorize cubic binomials. In this article we will go over the different aspects of formula a3-b3 together with examples that have been solved and the meaning that is involved.

What is a^3 – b^3 Formula?

The formula for a ³– 3 ³ formula, also known as the difference in cubes formula is as is:

a3 – b3 = (a – b) (a2 + ab + b2)

You can recall these signs with the help of this trick.

“a cube minus b cube formula” can be confirmed by multiplying (a + B) as well as (a2 + ab + B2) and then determining if you can get a3 + 3.

Proof of a Cube Minus b Cube Formula

Let’s verify the cubes minus the cubes formula. To establish that the formula of ^three– 3 = ^3.= (a + B) (a ² + ab + b ²) we must demonstrate here LHS + RHS. Let’s start with the following steps.

LHS = a ³– b ³

On Solving RHS side we get,

= (a – b) (a² + ab + b²)

By multiplying a and b independently by (a ² + ab + b ²) we will get

= a (a² + ab + b²) – b(a² + ab + b²)
= a3 + a2b + ab2 – a2b – ab2 – b3
= a3 + a2b – a2b + ab2- ab2 – b3
= a³ – 0 – 0 – b³
= a³ – b³

This is how it was proved: LHS = RHS

Also Check: a^3+b^3 Formula

Examples on a^3 – b^3 Formula

Let’s learn the ³ – ³ formula using a few solutions.

Exemple 1. Calculate the value of ³ 8. ³ by applying the a3 ^formula.– b3 formula.

Solution:

To find the following: To find: ³ 8. ^3..

Let’s assume that A = 108 and B = 8.

We will substitute these into the formula of 3 – b ³ 3 – b ^3..

a³ – b³ = (a – b) (a² + ab + b²)

108³ – 8³ = (108 – 8) (108² + (108)(8) + 8²)

= (100) (11664+864+64)

= (100) (12592)

=1259200

Answer: 108³ – 8³ = 1,259,200.

Example 2. Calculate the formula 27x ³ (125) using the a3 Formula – b3.

Solution:

To factorize to factorize: 27 x ³ + 125.

We will apply the formula a ^3. – ³formula to calculate this.

The expression given as

27x³ – 125 = (3x)³ – 5³

We will replace for a = 3x, and 5 in the formula the formula of ^3. – ^3..

a³ – b³ = (a – b) (a² + ab + b²)

(3x)³ – 5³ = (3x – 5) ((3x)² + (3x)(5) + 5²)

= (3x – 5) (9x² + 15x + 25)

Answer: 27x³ – 125 = (3x – 5) (9x² + 15x + 25).

3. Reduce 19 ³ 20 ³ by using a cube plus the formula for b cubes.

Answer: To find 19 ³ – 20 ³

Let’s say that a = 19 and b = 20

Using formula a³ – b³ = (a – b) (a² + ab + b²)

We will replace these in the formula of a ³ 3 – ³ formula.

a³ – b³ = (a – b) (a² + ab + b²)

19³ – 20³ = (19 – 20) (19² + (19)(20) + 20²)

= (-1) (361 + 380 + 400)

= (-1) (1141)

= -1141

Answer: 19³ – 20³ = -1141.

FAQ’s on a^3 – b^3 Formula

What is the Expansion of a ³– b ³ Formula?

A ^3.– 3 ^3. formula can be described as a cube less the cube. Its expansion can be expressed in terms of ^3.– 3 ^3. = (a + (a -) (a ² + ab + ^2.).

What is the a ³– b ³ Formula in Algebra?

The three-b-3 ³– B ³ formula is also referred to for being one of the key algebraic identities. It can be read as a cube plus the cube. The formula a3 – B3 is A3 – B3 = (a + (b) (a2 + ab + ab +).

How to simplify the calculation of numbers by using Cube ^{What is a cube?}– B cube Formula?

Let’s look at the application of the ³3 – ^3. formula by taking advantage from the example below.

Example: Find the sum of 103-23 using the a3-b3 formula.

To calculate 10, ³ – 2 ³ Let us suppose that A = 10 and B = 2.

We will substitute these into the formula 3 – b ³ 3 – b ^3..

a³ – b³ = (a – b) (a² + ab + b²)
10³ – 2³ = (10 – 2) (10² + (10)(2) + 2²)
= (8) (100 + 20 + 4)
= (8)(124)
= 992

Answer: 10³ – 2³ = 992.

What are the Applications of a^3 – b^3 Formula?

The a cubed minus cubed formula is employed to:

Factorize algebraic expressions. Example: x³ – 27 = x³ – 3³ = (x – 3) (x² + 3x + 9)

Reduce trigonometric expressions. Example: sin³x – cos³x = (sin x – cos x) (sin²x + sin x cos x + cos²x) = (sin x – cos x) (1 + sin x cos x)

What are a3 and b3 and a3 + B3 formulas?

a^3 – b^3 = (a – b) (a^2 + ab + b^2)

a^3 + b^3 = (a + b) (a^2 – ab + b^2)

It is important to note that in all of these formulas the sign between the letters a and b is the same symbol that is on the left. ab represents the opposite sign while b2 will always be positive.

How to Use the a ³– b ³ Formula Give Steps?

The steps below are to be performed using the cube minus cube formula.

For starters, look at the pattern of the numbers regardless of whether the numbers have 3 for power.

Also, write down the formula of a3 3 – b3 : a3 – 3 = (a + ab + b) (a2 + ab ab +)

Then, replace both the a and b within the cubed ^formula. cubed formula, and simplify.

What is a Cube Minus b Cube Minus c Cube Formula?

We can derive our formula to calculate a cube plus the cube of b and c with the help of the formula a3 B3 + 3abc – c3 is (a + b c)(a2 + b2 C2 ab – bc + ca) by putting ab = -b, and c = -c into. Then we get

A3 + (-b)3 + (-c)3 – 3a(-b)(-c) = (a + b – c)(a2 + (-b)2 + (-c)2 – a(-b) (-c) (-b)(-c) (-c) (-c)a)

a3 – b3 – c3 – 3abc = (a – b – c)(a2 + b2 + c2 + ab – bc + ca)

By adding 3abc on both sides:

a3 – b3 – c3 = (a – b – c)(a2 + b2 + c2 + ab – bc + ca) + 3abc

Also Read: Derivation Of a-b Whole Cube

a^3 – b^3 Formula

Cube – B Cube Formula

The a cube – cube formula i.e. the ³ 3 – ³ formula, is known as”the difference formula of cubes” in mathematics. This formula is thought of as part of mathematical identity within math.

This formula can be used to calculate the difference between 2 cubes, without even calculating the cubes. The formula of 3 – b ³ – 3 + ³ can also be employed to calculate binomials as cubes.

In this article, you’ll be taught the cube minus cube formula as well as examples and proof.

a^3 – b^3 Formula

The formula for the equation a ^three – ^3. is defined in terms of the multiplicative power of binomial as well as a trinomial. This formula is used to analyze the numerical and polynomial expressions.

The formula for 3 – b ³ – ^3. is described by:

a3 – b3 = (a – b)(a2 + ab + b2)

Let’s examine the evidence for this formula.

A cube A cube formula Proof

To prove: a³ – b³ = (a – b)(a² + ab + b²)

Consider LHS = a ³ – b ³

RHS = (a – b)(a² + ab + b²)

The differences between numbers A ^three and the b ³ formula can be determined by using the RHS.

RHS = (a – b)(a² + ab + b²)

= = a (a² + ab + b²) – b(a² + ab + b²)

= a3 + a2b + ab2 – a2b – ab2 – b3

= a3 + a2b – a2b + ab2- ab2 – b3

= a³ – 0 – 0 – b³

= a³ – b³

= LHS

Therefore, a ³ – b ³ = (a – b)(a ² + ab + b ²)

Thus, it was it was proved.

Solved Examples

Example 1: Evaluate: 103 ³ – 27

Solution:

103³ – 27

= 103³ – 3³

This is the form 3 – b ^3. – 3. ^3..

Utilizing the formula a ^3. – B ^3. equals (a + b)(a ² + ab + ^2.),

1033 – 27 = 1033 – 33 = (103 – 3)[(103)2 + (103)(3) + (3)2]

= 100(10609 + 309 + 9)

= 100 (10927)

= 1092700

Therefore, 103³ – 27 = 1092700

Examples 2 Factorize 64x ³ + the cube by using a cube less the formula for b cubes.

Solution:

64x³ – 216

= (4x)³ – (6)³

This is the form A ^3. – 3. ^3..

By using the formula ^3. – 3 – ^3. equals (a ab – b)(a ² + ab + ^2.),

64x³ – 216 = (4x – 6)[(4x)² + (4x)(6) + (6)²]

= (4x – 6)(16x² + 24x + 36)

Therefore, 64x³ – 216 = (4x – 6)(16x² + 24x + 36)

Here, we’re going to look at the formula used to calculate

a³ – b³

We already know the formula or expansion for (a – B) ³.

That is,

(a – b)³ = a³ – b³ – 3ab(a – b)

Case 1 :

(a – b)³ = a³ – b³ – 3ab(a – b)

Add 3ab(a – 3ab(a -) on each side.

(a – b)³ + 3ab(a – b) = a³ – b³

So it follows that the formula (a ³ – B ³) is

a³ – b³ = (a – b)³ + 3ab(a – b)

Case 2 :

From the first case

a³ – b³ = (a – b)³ + 3ab(a – b)

a³ – b³ = (a – b)[(a – b)² + 3ab]

a³ – b³ = (a – b)[a² – 2ab + b² + 3ab]

a³ – b³ = (a – b)(a² + ab + b²)

So it follows that the formula (a ³ – B ³) is

a3 – b3 = (a – b)(a2 + ab + b2)

So,

(a – B) as well (a ² + ab + ^2.)

are the determinants are the factors (a ³ – are the factors of (a 3 – ^3.).

Note :

Based on our needs We can either apply the formula for the case 1 or 2, for (a ³ – 3. ^3.).

Also Read: A Plus B Whole Square & Cube

FAQ’s on a^3 – b^3 Formula – A Cubed minus B Cubed –

Practice Questions

Question 1 :

Factor :

x³ – 1

Solution :

Create (x ³ – 1) in the form of (a ³ – 3 – ^3.).

x³ – 1 = x³ – 1³

(x3 13) is the equivalent of (a3 – B3).

Comparing (a3 – the b3) and (x3 13) We are able to get

A = x

B = 1

Write down the formula for (a ³– 3 b ^3.) as shown in the case 2.

a³ – b³ = (a – b)(a² + ab + b²)

Substitute x for A and 1 for.

x³ – 1³ = (x – 2)(x² + x(1) + 1²)

3 + 1 = (x ³ + 1 = (x + 1)(x ² + 1 +)

Question 2 :

Factor :

8x³ – 27y³

Solution :

Note: Write (8x ³ – 27y ³) in the form of (a ³ – 3 – ³).

8x³ – 27y³ = (2x)³ – (3y)³

(2x) ³ (3y) (3y) ³is in the form of (a ³– 3). ³).

Comparing (a3 – B3) or (2x)3 – (3y)3 We can obtain

A = 2x

Also Read: Types of A Specific Formula for Solving a Problem Is Called

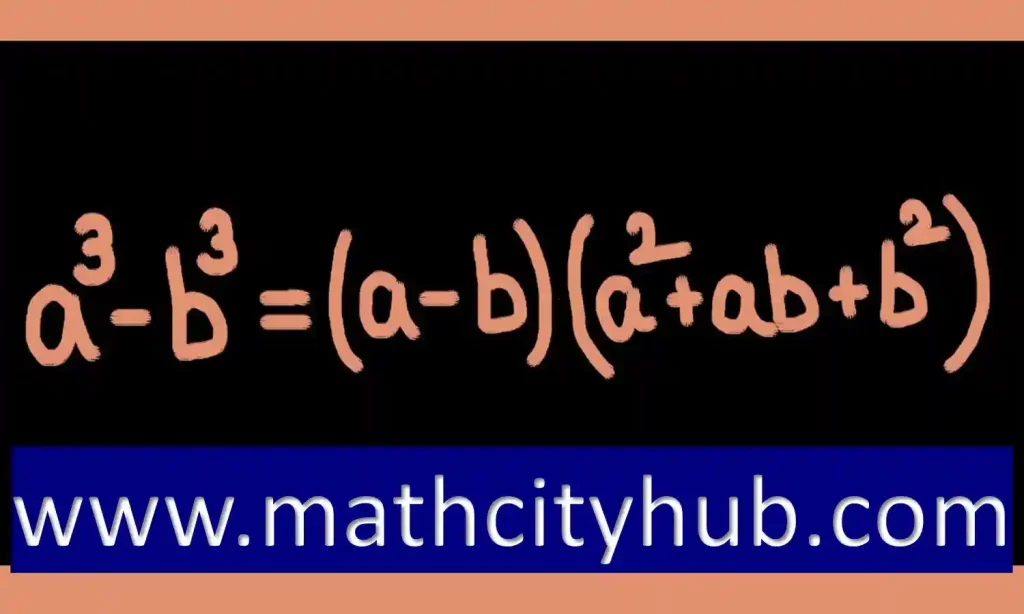
1. How do I find the mathematical formula of “A cubed minus B cubed”?
2. Do you know how to simplify the expression “A cubed minus B cubed”?
3. How can the expression “A cubed minus B cubed” extended?
4. If A is 5, and B is 2 What is the value of A cubed and B cubed?
5. Does “A cubed minus B cubed” equivalent to “(A minus B) cubed”? What is the reason or reason?
6. Do you know how to factorize the expression “A cubed minus B cubed”?
7. What happens when you do “A cubed minus B cubed” when A and B are identical?
8. What does “A cubed minus B cubed” compare to “B cubed minus A cubed”?
9. Are there any specific properties or formulas relating in “A cubed minus B cubed”?

Sure! Here are some of the questions to ask about A cubed and B cubed