A Plus B – (a + b)3 Formula: Here, we shall discuss the algebraic formula (a + b)3, its proof derivative, and some examples.
This is among the most crucial and fundamental algebraic formulas, which are more important in competitive exams such as NTSE, NDA, AFCAT, SSC, Railways, etc.
It also helps school students, particularly class 10th, make math calculations more quickly.
(a + b)3 Formula
Let’s say a and b are two variables that represent two algebraic terms. If you add each of them, it is expressed as A+B within Algebra.
It’s not only an algebraic expression, but also it provides a Binomial algebraic equation. The cube that results from the algebraic terms a and B is formulated by the formula (a+b)3 with the mathematical formula below.
(a + b)3 = a3 + b3 + 3ab(a + b)
A plus b cube (a + b)3 is equivalent to the cube of that of the cube three times the products of A, B plus the product of a, and the sum of a plus.
(a + b)3 = a3 + b3 + 3a2b + 3ab2
The a+b cube (a + b)3 algebraic formula is typically used to determine the cube of a binomial equation where two algebra terms are specified.
It can also be utilized to create the factors of various kinds of trinomial equations where three algebraic terms are specified.
This formula for a+b whole cubes is also known as”the cube of the rule of the sum of two terms as well as it is also known as the binomial cube identification and the Binomial Product Formula.
A + B Whole Cube Formula Proof
To calculate the binomial cube equation, we must increase the number of times three for algebraic equations with two terms similar to (a + b)(a + b)(a + b) = (a + b)3. The formula for a + b as a whole cube (a + b)3 is also an algebraic identity in math. It is the (a + b)3 formula constructed by,
Also Read: Formula For Solving A Problem Is Called
(a + b)3 = (a + b)(a + b)(a + b)
= (a2 + 2ab + b2)(a + b)
= a3 + a2b + 2a2b + 2ab2 + ab2 + b3
= a3 + 3a2b + 3ab2 + b3
= a3 + 3ab(a+b) + b3
Thus, the a+b cube (a + b)3 formula can be determined as
(a + b)3 = a3 + 3a2b + 3ab2 + b3
A + B Whole Cube Formula with Examples
If you can memorize this a+ B whole cube formula, you’ll be able to quickly figure out the answer to the binomial algebraic term in math.
Below are some examples to help you understand the complexities of this formula: a+b total cube.
Questions 1 and 2. Determine an algebraic formula using the aid of an appropriate mathematical identity, or a procedure (3x + 2y)3
Answer: Given that the equation (3x + 2y)3 has two algebraic words, it is binomial.
By using (a + b)3 Algebraic Formula,
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(3x + 2y)3 = (3x)3 + 3 x (3x)2 x 2y + 3 x (3x) x (2y)2 + (2y)3
(3x + 2y)3 = 27×3 + 54x2y + 36xy2 + 8y3
Question 2: Determine the expression 8×3 + y3 if the sum of 2x and y is 6, and xy = 2.
Answer: Given that the equation (8×3 + y3) has two algebraic words, it’s a binomial equation.
Based on the question 2x + y = 6, 2x = 2.
By using (a + b)3 Algebraic Formula,
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Here a = 2x; b = y
So,
(2x + y)3 = (2x)3 + 3 x (2x)2 x (y) + 3 x 2x x (y)2 + (y)3
(2x + y)3 = 8×3 + 12x2y + 6xy2 + y3
When we put the value of 6 + 2x = have
63= 8×3 + 6xy(2x + y) + y3
When we take a xy value equal to 2, we will get
216 = 8×3 + 6 x 2 x 6 + y3
8×3 + y3 = 144
Question 3: Determine the value of an expression by using the formula: (a + b)3 formula: (2x + 5y)3
Answer: With the help of (a + b)3 Formula,
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Here, a = 2x and b = 5y.
(2x + 5y)3 = (2x)3 + 3 x (2x)2 x 5y + 3 x (2x) x (5y)2 + (5y)3
(2x + 5y)3 = 8×3 + 60x2y + 150xy2 + 125y3
4th Question: Determine the worth of the expression by using the (a + b)3 formula: (7x + 11y)3
Answer: With the help of (a + b)3 Formula,
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Here, a = 7x and b = 11y
(7x + 11y)3 = (7x)3 + 3 x (7x)2 x 11y + 3 x (7x) x (11y)2 + (11y)3
(7x + 11y)3 = 343×3 + 1617x2y + 2541xy2 + 1331y3
Questions 5 and 6: Determine the value from the equation below applying (a + b)3 identity: (5x + 9y)3
Solutions: With the help of (a + b)3 Formula,
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Here, a = 5x and b = 9y.
(5x + 9y)3 = (5x)3 + 3 x (5x)2 x 9y + 3 x (5x) x (9y)2 + (9y)3
(5x + 9y)3 = 125×3 + 675x2y + 405xy2 + 729y3
Also Read: Types of A Specific Formula for Solving a Problem Is Called
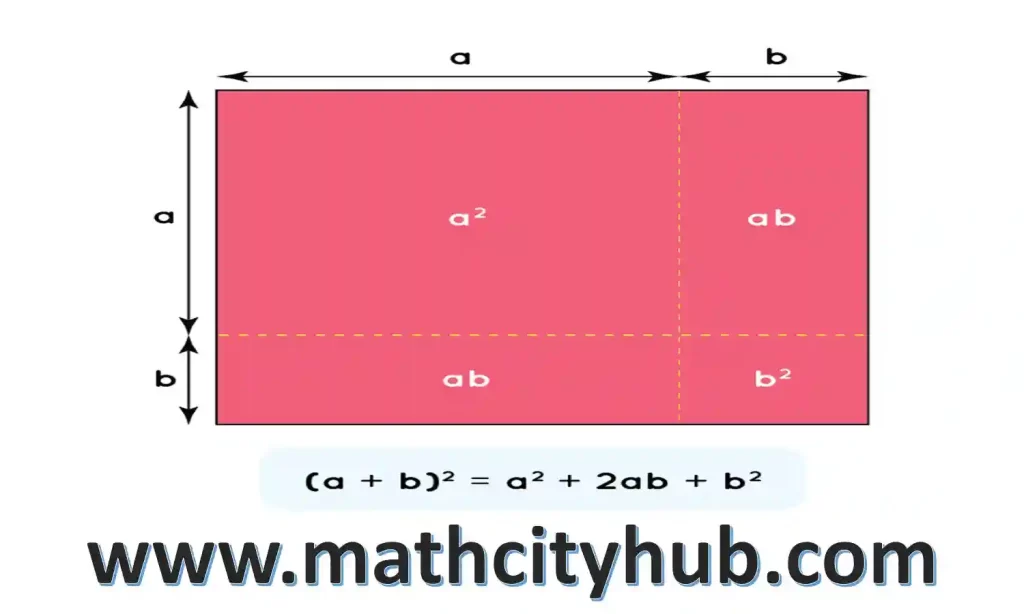
A Plus B Whole Square
Are you searching for an additional b ka square? It is possible to check the formulas for the plus b ka complete court using three methods.
We will discuss our (a+b)^2 algebra formulas to help you understand how to construct (A+B)^2 and the proof.
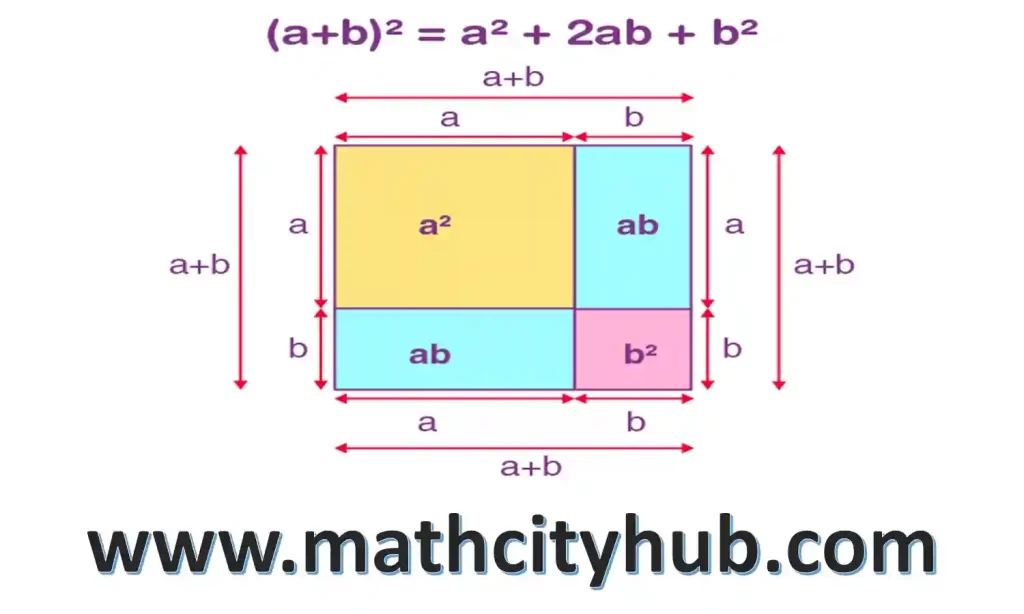
(a+b)2=(a+b)(a+b)
=>(a+b)(a+b)=a(a+b)+b(a+b)=a2+ab+ba+b2
=>(a+b)2=a2+2ab+b2
(A+B)^2 Verifications
Verify your identity using A=3 and B= 4.
place an amount of b into LHS
(a+b)2=(3+4)2
=>72=49
Put on the values of A and B into RHS
=>(a+b)2=a2+2ab+b2
=>32+2x3x4+42
=>9+24+16=>49
Therefore LHS=RHS
Proof Formulas (a+b)2=a2+2ab+b2
a Plus b, Squared
You can ask the high school math teacher to identify the one error made by a student across all grades, which is the most enraged.
The most frequent answer you’ll get is a variation of the way students put the two sums of figures (as in (a + b)2) to find the sum of squares of the numbers (as in A2 + B2).
However, these expressions are different; that’s different from the way the squaring process works. Students who understand why they’re not equal are more likely to be successful in the future.
This lesson will attempt to understand this disparity:
Before explaining why it’s false, knowing why so many people believe it is factual is crucial.
There are many reasons a student could believe it’s the case, and each of them has their own reasoning.
Also Read: Derivation of A Square Minus B Square With Example
Before explaining why it isn’t true, I think it’s important to understand why so many people think it is true.
There are several reasons a student might think it’s true, and each of those reasons has its own logic.
(1) I know it’s true for multiplication:
so why isn’t it true if the symbol between them is addition instead?
This is a classic case of a student paying more attention to the notation than to what the symbols actually mean. Squaring means multiplying an expression times itself: (ab)2 means (ab)(ab).
But crucially, that’s a whole bunch of multiplications. And we all know that you can regroup and rearrange items being multiplied at will (formally, we say that multiplication is associative and commutative).
And when you do regroup and rearrange, you see there are two a‘s and two b‘s all multiplied together; thus a2b2. But look at what (a + b)2 means: (a + b)(a + b).
Where’s the possibility for rearranging so simply? It’s not there. The mixture of plus and times makes this expression harder to work with than if it’s all multiplication.
Certainly! Here are some questions about the formula “a plus b”:
- What does the formula “a plus b” represent?
- How would you simplify the expression “a plus b”?
- Can you provide an example of substituting values for “a” and “b” in the formula “a plus b”?
- Are there any restrictions or limitations when using the formula “a plus b”?
- What is the result of “a plus b” if “a” equals 5 and “b” equals 3?
- How does the formula “a plus b” differ from the formula “b plus a”?
- Can you explain the commutative property of addition in relation to the formula “a plus b”?
- In the formula “a plus b,” is it possible for “a” and “b” to have different units or dimensions?
- How would you graph the formula “a plus b” on a coordinate plane?
- Are there any alternative notations or symbols used to represent the formula “a plus b”?
- Can you describe any real-life scenarios or applications where the formula “a plus b” is used?
- What happens when “a” and “b” are both negative numbers in the formula “a plus b”?
- Is it possible for “a” and “b” to be variables or unknowns in the formula “a plus b”?
- Does the formula “a plus b” have any mathematical properties or special characteristics?
- Can you rewrite the formula “a plus b” using mathematical symbols or notation?
- How does the formula “a plus b” relate to other arithmetic operations like subtraction, multiplication, and division?
- Are there any specific strategies or techniques to simplify or manipulate the formula “a plus b” in algebraic expressions?
- What is the difference between the formula “a plus b” and the concept of addition as a mathematical operation?
- Can you provide a proof or justification for the formula “a plus b” using mathematical reasoning?
- How does the formula “a plus b” extend to higher dimensions or more complex mathematical structures?
If You want to GET FREE PDF BOOKS. Please CLICK HERE