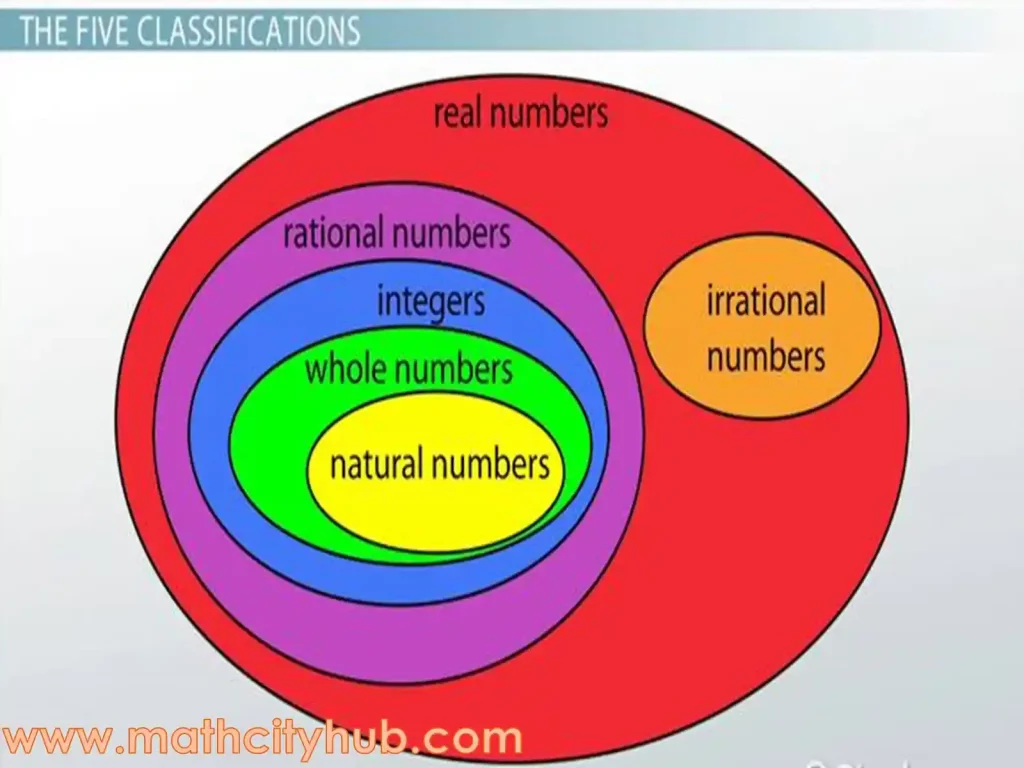
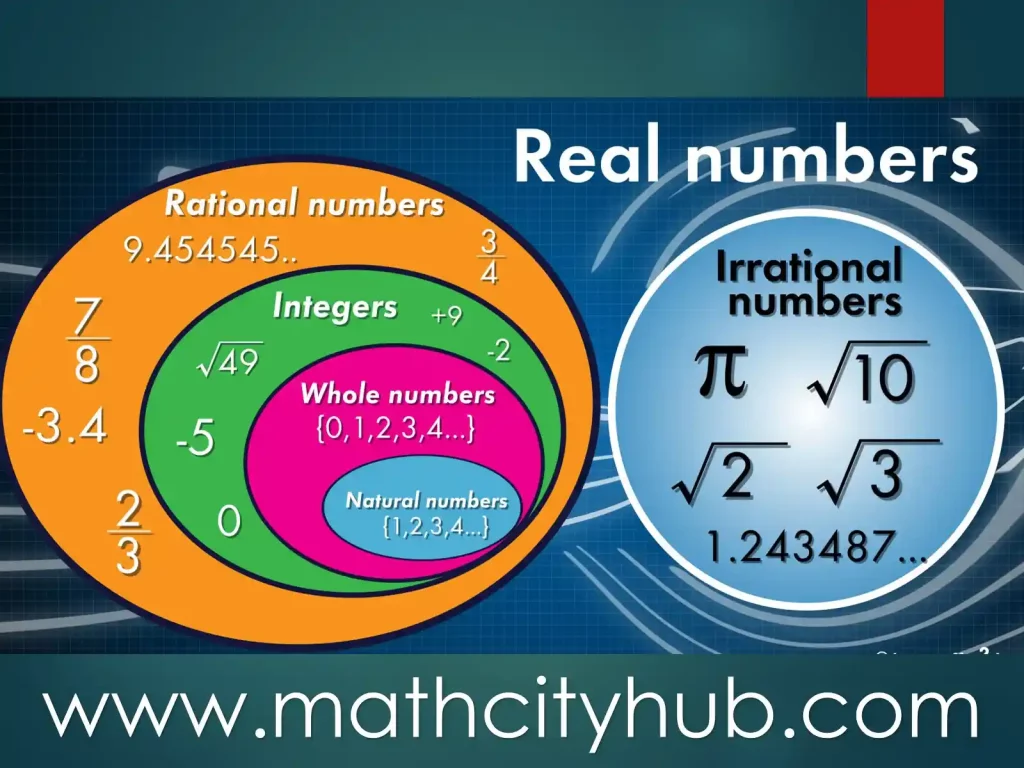
Exercise.2.1: Real Numbers

Exercise.2.1: Real numbers form a fundamental and expansive set within the realm of mathematics, encompassing a wide spectrum of numerical values with diverse properties.

Unlike discrete sets like natural numbers or integers, the set of real numbers is continuous and unbounded, extending from negative to positive infinity. Real numbers include familiar integers, fractions, decimals, and even irrational numbers, providing a comprehensive framework for representing quantities in a precise and continuous manner.

The study of real numbers is essential in various mathematical disciplines, playing a pivotal role in calculus, analysis, geometry, and beyond. In this vast and versatile set, each real number finds its place on the number line, contributing to a rich and interconnected tapestry that underlies many mathematical concepts and real-world applications.

Understanding real numbers is not only integral to advanced mathematical studies but also crucial for modeling and interpreting the complexities of the physical world.

Neutral number:

Neutral numbers, also known as natural numbers, are a set of positive integers starting from 1 and extending infinitely. They are commonly used for counting and ordering. The set of natural numbers is denoted by the symbol

N or sometimes

Mathematically, the set of natural numbers is expressed as follows:

N={1,2,3,4,5,…}

And so on. Natural numbers are used for counting objects, ordering items, and representing quantities in a non-negative, whole number format. They serve as the foundation for other sets of numbers, such as integers, rational numbers, and real numbers.

Exercise.2.1: Real Numbers, all real numbers are solutions, ordering real numbers, which rational expression is defined for all real numbers, comparing real numbers,

Whole Number:

Whole numbers are a set of non-negative integers, including zero and all the positive integers without any fractional or decimal parts. In other words, whole numbers consist of the natural numbers (1, 2, 3, …) along with zero (0). Exercise.2.1:

Mathematically, the set of whole numbers is expressed as follows:

Whole Numbers

Whole Numbers={0,1,2,3,4,…}

Definition of Integers:

An integer is a whole number that can be positive, negative, or zero. It does not include any fractional or decimal parts. Integers are denoted by the symbol ℤ.

Examples of Integers:

-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …

Examples of Numbers that are Not Integers: Exercise.2.1:

-1.5, -0.25, 3/4, π (approximately 3.14), √2 (approximately 1.41), …

Properties of Integers:

Integers are closed under addition, subtraction, and multiplication. This means that the sum, difference, and product of two integers are always integers.
Integers are not closed under division. The quotient of two integers may be a fraction or a decimal, which are not integers.
Integers are ordered from least to greatest. This means that we can compare any two integers and determine which one is smaller or larger.
Applications of Integers:
Integers are used in many different areas of mathematics, including:
Arithmetic
Algebra
Geometry
Number theory
Integers are also used in many real-world applications, such as:
Counting objects
Measuring distances
Keeping track of time
Representing money

A rational number.

A rational number is any number that can be expressed as a fraction of two integers, where the denominator is not zero. In other words, a rational number is any number that can be written in the form p/q, where p and q are integers and q ≠ 0.
Examples of rational numbers:
1/2
3/4
-5/6
10
-1
0
Types of rational numbers:
Proper fractions: A proper fraction has a numerator that is smaller than its denominator. For example, 1/2, 3/4, and -5/6 are all proper fractions. Exercise.2.1:
Improper fractions: An improper fraction has a numerator that is larger than or equal to its denominator. For example, 10, -1, and 0 are all improper fractions.
Whole numbers: Whole numbers can be written as a fraction with a denominator of 1. For example, 10, -1, and 0 are all whole numbers.
Properties of rational numbers:
Rational numbers can be added, subtracted, multiplied, and divided.
Rational numbers can be compared to each other using the symbols <, >, =, ≤, and ≥.
Rational numbers can be ordered from least to greatest.
Examples of how rational numbers are used in everyday life:
When you measure the length of something, you are using a rational number. For example, if you measure the length of a piece of wood and find that it is 1/2 meter long, you are using the rational number 1/2.
When you cook a recipe, you are using rational numbers. For example, if a recipe calls for 1/4 cup of sugar, you are using the rational number 1/4.
When you play a game, you are using rational numbers. For example, if you are playing a game of basketball and you score 3 points out of a possible 4 points, you have scored 3/4 of the points.
An irrational number is a real number that cannot be expressed as a ratio of two integers. In other words, an irrational number is any number that cannot be written in the form p/q, where p and q are integers and q ≠ 0.
Examples of irrational numbers:
√2
√3
π
e
Properties of irrational numbers:
Irrational numbers cannot be expressed as a ratio of two integers.
The decimal expansion of an irrational number is neither terminating nor repeating.
Irrational numbers are not closed under addition, subtraction, multiplication, or division.
Examples of how irrational numbers are used in everyday life:
When you calculate the area of a circle, you are using the irrational number π.
When you calculate the compound interest on a loan, you are using the irrational number e.
When you study the behavior of waves, you are using irrational numbers.
Irrational numbers are an important part of mathematics, and they are used in many different fields of study. Exercise.2.1:
A real number is any number that can be represented on a number line. Real numbers include rational numbers, irrational numbers, and all the numbers between them. In other words, any number that we can think of, except imaginary numbers, is a real number.
Examples of real numbers:
1/2
√3
π
e
-10
0
10
Types of real numbers:
Rational numbers: Rational numbers can be expressed as a ratio of two integers, where the denominator is not zero. For example, 1/2, √3, and -5/6 are all rational numbers.
Irrational numbers: Irrational numbers cannot be expressed as a ratio of two integers. For example, π and e are both irrational numbers.
Algebraic numbers: Algebraic numbers are the solutions to polynomial equations with integer coefficients. For example, √2 is an algebraic number because it is the solution to the equation x^2 – 2 = 0.
Transcendental numbers: Transcendental numbers are not the solutions to any polynomial equation with integer coefficients. For example, π is a transcendental number.
Properties of real numbers:
Real numbers can be added, subtracted, multiplied, and divided.
Real numbers can be compared to each other using the symbols <, >, =, ≤, and ≥.
Real numbers can be ordered from least to greatest.
Examples of how real numbers are used in everyday life:
When you measure the length of something, you are using a real number. For example, if you measure the length of a piece of wood and find that it is 1.5 meters long, you are using the real number 1.5. Exercise.2.1:
When you cook a recipe, you are using real numbers. For example, if a recipe calls for 2/3 cup of flour, you are using the real number 2/3.
When you play a game, you are using real numbers. For example, if you are playing a game of basketball and you score 3 points out of a possible 4 points, you have scored 0.75 of the points.

A terminating decimal fraction is a decimal number with a finite number of digits after the decimal point. In other words, the digits after the decimal point eventually end, and there are no repeating patterns. For instance, 0.25, 0.687, and 1.9999 are all terminating decimal fractions.

These numbers can be expressed as a fraction with a denominator that is a power of 10. For example, 0.25 can be written as 25/100 or 1/4, 0.687 can be written as 687/1000 or 229/333, and 1.9999 can be written as 19999/10000 or 9999/5000.

Terminating decimal fractions are considered rational numbers, meaning they can be represented as a ratio of two integers.

This is because they can be converted into a fraction with a denominator that is a power of 10, which is essentially a multiple of 2 and 5, the only prime factors allowed in the denominator of a rational number that terminates after the decimal point.

Here’s a summary of the characteristics of terminating decimal fractions:

Finite number of digits after the decimal point: The digits after the decimal point eventually end.

No repeating patterns: There are no repeating sequences of digits after the decimal point.

Expressible as a fraction: Can be represented as a fraction with a denominator that is a power of 10.

Rational numbers: Belong to the category of rational numbers.

A recurring and non-terminating decimal fraction is a decimal number with an infinite number of digits after the decimal point, and some or all of these digits repeat indefinitely.

In other words, the digits after the decimal point keep repeating forever, forming a pattern that never ends. Examples of recurring and non-terminating decimal fractions include 0.333333…, 0.121212…, and 0.777777….

These decimals represent rational numbers, which means they can be expressed as a fraction of two integers. However, unlike terminating decimal fractions, recurring and non-terminating decimal fractions cannot be directly converted into a simple fraction with a denominator that is a power of 10.

Instead, they require a more sophisticated method of conversion, which involves setting up two equations and solving for the unknown fraction. Exercise.2.1:

Here’s a summary of the characteristics of recurring and non-terminating decimal fractions:

Infinite number of digits after the decimal point:

The digits after the decimal point never end.

Repeating pattern: Some or all of the digits after the decimal point repeat indefinitely.

Expressible as a fraction: Represent rational numbers, but require a more complex conversion method.

These decimals have various applications in mathematics and science, particularly in areas like number theory, calculus, and physics. They also play a role in everyday life, such as in calculations involving percentages, interest rates, and currency conversions.

Here are some questions and answers about real numbers:

1. What is a real number?

• Answer: A real number is a mathematical quantity that can represent a position along a line. It includes both rational and irrational numbers and can be positive, negative, or zero.

2. What is the difference between rational and irrational numbers?

• Answer: Rational numbers can be expressed as the quotient or fraction of two integers, while irrational numbers cannot be expressed as fractions and have non-repeating, non-terminating decimal expansions.

3 Can a real number be both rational and irrational?

Answer: No, a real number cannot be both rational and irrational. A number is either rational or irrational, but not both.

4 Is zero a rational number?

Answer: Yes, zero is a rational number because it can be expressed as the fraction

5 What is the decimal representation of a terminating decimal?

Answer: A terminating decimal is a decimal that has a finite number of digits. For example,

0.25

0.25 is a terminating decimal.

6 Give an example of a non-terminating, repeating decimal.

Answer:

0.333…

0.333… is a non-terminating, repeating decimal representing the fraction .