Welcome to the intricate world of mathematics, where numbers weave a tapestry of relationships. In this exploration, we unravel the concept of the Least Common Multiple (LCM), a fundamental element in number theory.
The LCM, often abbreviated yet profoundly impactful, plays a pivotal role in solving mathematical puzzles and real-world problems. This journey will demystify the LCM, offering insights into its significance and practical applications.
Whether you’re a student navigating the complexities of arithmetic or a curious mind seeking mathematical enlightenment, this introduction sets the stage for a comprehensive understanding of the least common multiple.
Join us as we embark on a journey that transcends numerical theory and resonates in both academic and practical spheres.
Understanding the Least Common Multiple
Least Common Multiple Explained
The Least Common Multiple (LCM) is a crucial concept in number theory, offering a systematic approach to finding the smallest common multiple shared by two or more integers. It serves as a fundamental tool for simplifying fractions, solving equations, and navigating the intricate world of numbers.
To understand LCM, let’s consider two numbers, say a and b. The LCM of a and b is the smallest positive integer that is divisible by both a and b without leaving a remainder. In essence, it represents the least common denominator for these two numbers.
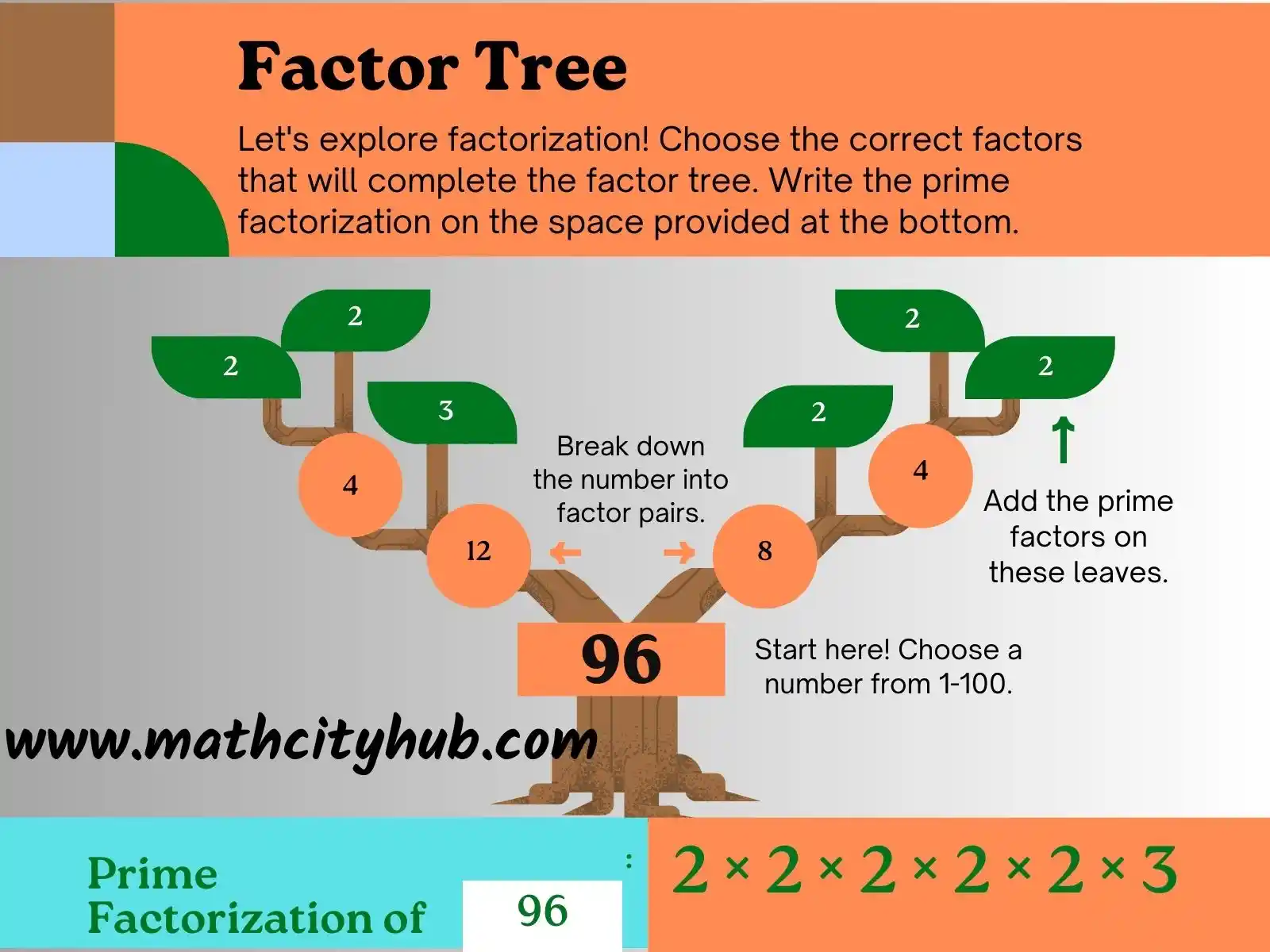
One method to calculate the LCM is through prime factorization. By expressing each number as a product of prime factors, we identify the common factors and their highest powers. Multiplying these highest powers yields the LCM.
Another approach involves listing the multiples of each number until a common multiple is found.
LCM plays a pivotal role in various mathematical scenarios. When working with fractions, the LCM of the denominators is crucial for finding a common denominator, facilitating addition, subtraction, and comparison of fractions.
In solving equations with multiple variables, LCM aids in simplifying expressions and finding a unified solution.
Beyond its theoretical importance, LCM finds practical applications in real-life scenarios. From scheduling tasks to coordinating events that repeat at different intervals, understanding and calculating the LCM ensures efficient planning and organization.
In essence, the Least Common Multiple is a versatile mathematical tool that simplifies complex calculations, fosters a deeper understanding of numerical relationships, and proves indispensable in both academic and everyday contexts.

The Significance of LCM in Mathematics
The Least Common Multiple (LCM) stands as a cornerstone in the realm of mathematics, holding immense significance and offering invaluable applications across various mathematical domains. Understanding its importance is pivotal for anyone navigating the intricacies of numerical relationships.
One key aspect of LCM lies in its role as a unifier. When dealing with fractions, the LCM of denominators serves as the common ground, allowing for seamless addition, subtraction, and comparison of fractions. This simplification is not only practical but also essential in various mathematical operations.
Moreover, LCM plays a pivotal role in solving equations with multiple variables. By identifying the least common multiple of coefficients, mathematicians can streamline expressions and find solutions that encompass all variables.
This capability extends the utility of LCM beyond basic arithmetic, making it an indispensable tool in algebraic endeavors.
In the realm of number theory, LCM provides insights into the relationships between integers. It allows mathematicians to explore the fundamental structure of numbers, revealing patterns and connections that contribute to a deeper understanding of mathematical principles.
The significance of LCM extends beyond the theoretical realm and finds resonance in practical applications. In scheduling and planning, LCM aids in coordinating events that recur at different intervals, ensuring efficient timing and organization. Its versatility in real-world problem-solving cements LCM as a practical and powerful mathematical concept.
In essence, the Least Common Multiple is more than just a mathematical abstraction; it’s a key that unlocks doors to efficient problem-solving, a tool that simplifies complex calculations, and a fundamental building block in the edifice of mathematical understanding.
Embracing the significance of LCM enriches one’s mathematical toolkit and empowers individuals to tackle mathematical challenges with precision and confidence.
Calculating the Least Common Multiple
Methods to Find the LCM
Unlock the mystery of finding the least common multiple with detailed insights into various methods. From the prime factorization method to the listing method, this section guides you through step-by-step procedures, ensuring a clear understanding of how to calculate LCM efficiently. Practical examples and scenarios bring these methods to life, making complex calculations more approachable.
Least Common Multiple vs. Greatest Common Divisor
Dive into the comparison between the least common multiple and the greatest common divisor (GCD). Understand the fundamental differences between these two mathematical concepts and grasp when and how to apply each. This section provides clarity on navigating these often-confusing terms, empowering you to tackle mathematical challenges with confidence.
Exploring Practical Applications
LCM in Real Life: Practical Examples
Witness the real-world applications of the least common multiple through practical examples. From scheduling tasks to understanding periodic phenomena, LCM plays a vital role in our daily lives. This section illustrates how this mathematical concept transcends the classroom, impacting various aspects of our routines and decision-making processes.
LCM in Problem Solving
Navigate through complex problem-solving scenarios where the least common multiple emerges as the hero. Uncover how LCM simplifies intricate problems, making them more manageable and solvable. This section equips you with problem-solving skills that extend beyond mathematics, fostering a mindset of efficiency and strategic thinking.
Questions & Answers
Understand the distinction between the least common multiple and the least common denominator. This FAQ clarifies common misconceptions and provides insights into when to use each term in various mathematical contexts.
Explore the realm of decimal numbers and grasp whether the concept of the least common multiple applies to them. This FAQ provides clarity on handling decimals in LCM calculations, offering valuable insights for precision in mathematical endeavors.
Delve into the practical implications of calculating the least common multiple for large numbers. This FAQ addresses concerns about computational challenges and provides strategies for handling extensive LCM calculations.
Uncover the connection between the least common multiple and effective time management. This FAQ explores how LCM principles can be applied to streamline schedules and enhance productivity in various aspects of life.
Expand your understanding of the least common multiple beyond the confines of mathematics. This FAQ explores the interdisciplinary applications of LCM, revealing its relevance in diverse fields and industries.
Take your LCM calculation skills to the next level with this FAQ, which introduces advanced techniques for handling complex scenarios. From multiple variables to non-integer values, discover strategies to tackle sophisticated LCM calculations.
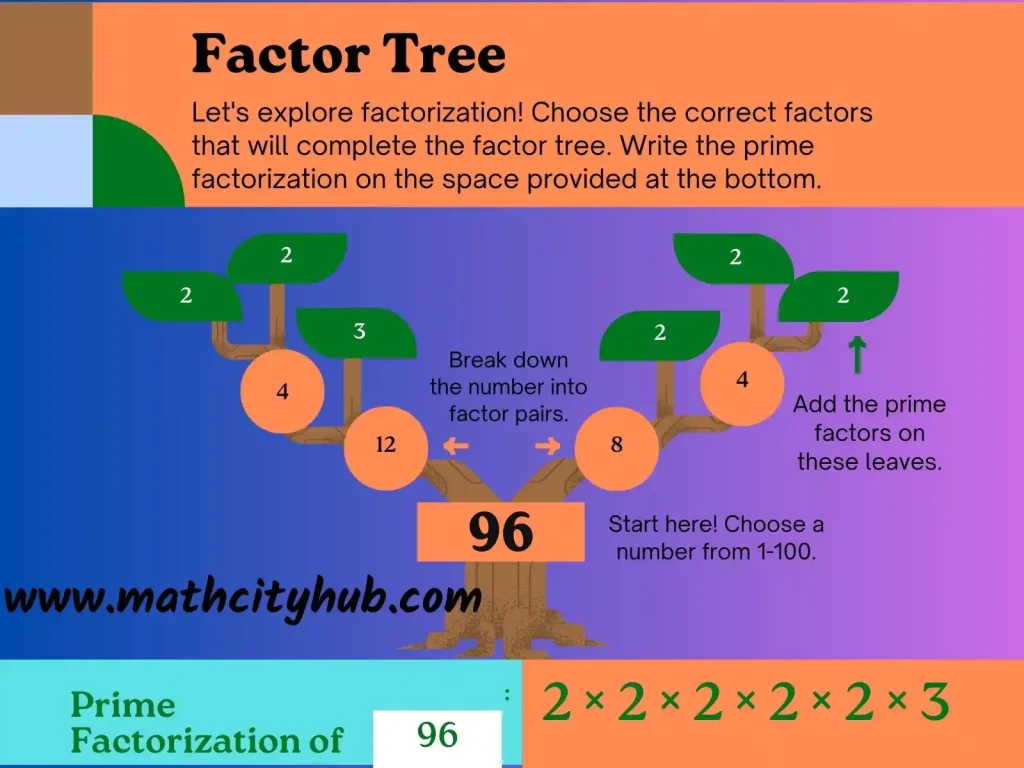
Conclusion
As we draw the curtain on our exploration of the Least Common Multiple (LCM), it becomes evident that this mathematical concept transcends mere numerical calculations—it forms the backbone of systematic problem-solving, decision-making, and efficient planning.
From its foundational definition as the smallest common multiple of two or more integers to its applications in real-life scenarios, the LCM proves to be a versatile and indispensable tool in the mathematician’s arsenal. Its ability to simplify fractions, unify equations with multiple variables, and contribute to a deeper understanding of numerical relationships showcases its far-reaching impact.
The LCM is not confined to the realms of theory; it seamlessly integrates into our daily lives. Whether we’re coordinating schedules, understanding periodic phenomena, or navigating complex problem-solving scenarios, the LCM emerges as a guiding principle, offering clarity and efficiency.
In conclusion, embracing the power of the Least Common Multiple enriches our mathematical journey, providing not only solutions to numerical puzzles but also fostering a mindset of precision and strategic thinking. As we continue to explore the intricate landscape of mathematics, the LCM stands as a beacon, illuminating the path to a deeper understanding of numbers and their profound interconnections.
Must Read:
Exercise.2.2: Properties of Real Numbers
Exercise.2.3: Radicals And Radicands
Exercise.2.4: Law of Exponents/ Indices
Exercise.2.6: Basic Operations on Complex Numbers
9th-Math-Ch-2-Review: Real And Complex Numbers
Exercise.3.1: Scientific Notation
Exercise.3.2: Common and Natural Logarithm
Exercise.3.3: Laws of Logarithm
Exercise.1.6: Solution Of Simultaneous Linear Equations
Exercise.1.5: Multiplicative Inverse a Of Matrices
Exercise.1.4: Multiplication Of Matrices
Azam Bodla
M.Phil. Mathematics, Content Writer, SEO Expert
Web Developer, Online Tutor
Call or WhatsApp: +923059611600
Gmail:azambodlaa@gmail.com