Basic Operations on Algebraic Fractions:Algebraic fractions, often encountered in intermediate and advanced mathematics, are expressions that involve both variables and constants in the form of fractions.
Understanding how to manipulate and perform basic operations on algebraic fractions is crucial for solving equations, simplifying expressions, and tackling more complex mathematical problems.
In this exploration of algebraic fractions, we will delve into the fundamental operations of addition, subtraction, multiplication, and division. Just as with numerical fractions, algebraic fractions follow certain rules and procedures that enable us to combine or simplify them effectively.
As we embark on this journey, it is essential to have a solid foundation in basic algebra and a familiarity with fraction arithmetic.
By mastering the operations presented in this guide, you will acquire valuable tools to navigate through algebraic expressions with ease, paving the way for a deeper understanding of mathematical concepts and problem-solving skills. Basic Operations on Algebraic Fractions:
So, let’s unravel the intricacies of algebraic fractions and empower ourselves to confidently manipulate these expressions in various mathematical scenarios.
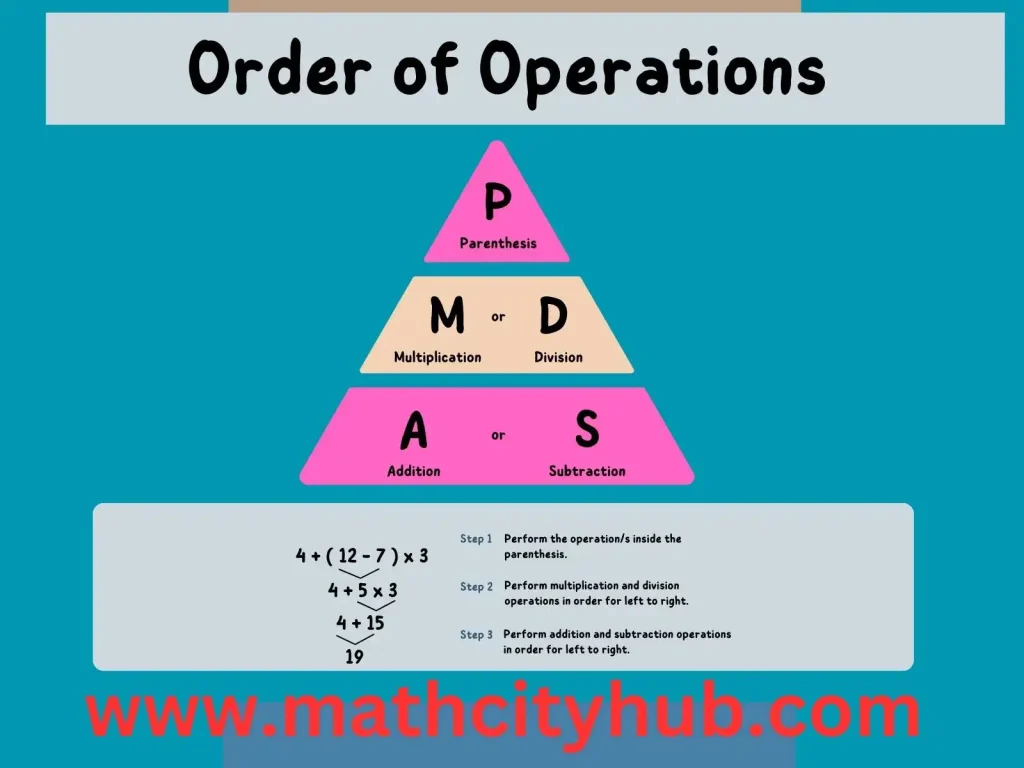
Explanation of Basic Operations on Algebraic Fractions:
Algebraic fractions involve expressions with both variables and constants in the form of fractions, and mastering basic operations on these fractions is essential for solving equations and simplifying complex expressions. Here’s a breakdown of the fundamental operations: addition, subtraction, multiplication, and division.
- Addition and Subtraction:
- When adding or subtracting algebraic fractions, it’s crucial to have a common denominator.
- Find the least common denominator (LCD) for the fractions involved. This is the smallest expression that both denominators divide into evenly.
- Adjust the fractions to have the common denominator and then perform the addition or subtraction on the numerators.
- Simplify the resulting fraction by factoring and canceling common factors in the numerator and denominator.
- Multiplication:
- To multiply algebraic fractions, simply multiply the numerators together and the denominators together.
- After multiplication, check for common factors in the numerator and denominator and cancel them out if possible.
- The result is the product of the algebraic fractions, presented in its simplest form.
- Division:
- Division of algebraic fractions involves multiplying by the reciprocal of the divisor.
- Invert the second fraction (the divisor) by swapping its numerator and denominator.
- Proceed to multiply the first fraction (the dividend) by the inverted form of the second fraction.
- Simplify the resulting fraction as you would in multiplication, canceling out common factors in the numerator and denominator.
Remember, maintaining a clear understanding of the rules for combining and simplifying algebraic fractions is vital for tackling more complex mathematical problems. These operations serve as the building blocks for various algebraic manipulations, laying the groundwork for advanced concepts in mathematics.
Practice and familiarity with these operations will contribute to a stronger foundation in algebra and better problem-solving skills.

Questions & Answers
: Algebraic fractions are expressions that involve both variables and constants in the form of fractions. Unlike numerical fractions, which consist only of numbers, algebraic fractions include variables, making them more versatile in representing mathematical relationships.
A2: Finding a common denominator is crucial because it allows us to combine fractions by creating a uniform base for comparison. This common ground facilitates addition or subtraction by ensuring that the fractions have the same denominator, making it possible to operate on their numerators.
A3: To add or subtract algebraic fractions, find the least common denominator (LCD), adjust the fractions to have this common denominator, and then perform the operation on the numerators. Finally, simplify the resulting fraction by canceling common factors in the numerator and denominator.
A4: To multiply algebraic fractions, multiply the numerators together and the denominators together. Afterward, simplify the resulting fraction by canceling common factors in the numerator and denominator.
A5: Division of algebraic fractions involves multiplying by the reciprocal of the divisor. Invert the second fraction by swapping its numerator and denominator, then proceed to multiply the first fraction by the inverted form of the second fraction. Simplify the result by canceling common factors in the numerator and denominator.
A6: Simplification is important in algebraic fractions to express the fractions in their simplest form. This involves canceling out common factors in the numerator and denominator, making the expression clearer and aiding in further mathematical operations.
A7: Mastering basic operations on algebraic fractions provides a solid foundation for solving equations, simplifying expressions, and tackling more complex mathematical problems. These operations serve as essential tools in manipulating algebraic expressions with confidence and efficiency.

Conclusion
In conclusion, a comprehensive understanding of basic operations on algebraic fractions is indispensable for navigating the intricacies of intermediate and advanced mathematics.
The ability to add, subtract, multiply, and divide algebraic fractions provides a powerful set of tools for solving equations, simplifying expressions, and addressing diverse mathematical challenges.
By emphasizing the importance of finding common denominators, performing operations with precision, and simplifying results, we equip ourselves with the skills necessary to handle complex algebraic expressions.
This proficiency not only enhances our problem-solving capabilities but also lays a robust foundation for tackling more advanced mathematical concepts.
As we conclude our exploration of algebraic fractions, it is evident that these fundamental operations play a pivotal role in shaping our mathematical reasoning.
The knowledge gained from manipulating algebraic fractions not only aids in academic pursuits but also fosters a deeper appreciation for the interconnected nature of mathematical concepts.
With a solid grasp of these operations, we empower ourselves to confidently engage with algebraic expressions, setting the stage for continued growth and success in the world of mathematics.
Must Read:
Exercise.2.2: Properties of Real Numbers
Exercise.2.3: Radicals And Radicands
Exercise.2.4: Law of Exponents/ Indices
Exercise.2.6: Basic Operations on Complex Numbers
9th-Math-Ch-2-Review: Real And Complex Numbers
Exercise.3.1: Scientific Notation
Exercise.3.2: Common and Natural Logarithm
Exercise.3.3: Laws of Logarithm
Exercise.1.6: Solution Of Simultaneous Linear Equations
Exercise.1.5: Multiplicative Inverse a Of Matrices
Exercise.1.4: Multiplication Of Matrices
Math 9th Full Book
Exercise #6.2
Azam Bodla
M.Phil. Mathematics, Content Writer, SEO Expert
Web Developer, Online Tutor
Call or WhatsApp: +923059611600
Gmail:azambodlaa@gmail.com






